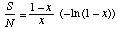
The purpose of this assignment is to become practiced at working with ecological datasets, and to learn about ecological diversity measures. We will begin our work with the small dataset from Brown Creek, and later tackle the much larger dataset from the TESC campus.
Ecologists and conservation biologists measure diversity for a number of reasons: (1) to characterize the community so that the ecological and evolutionary processes generating the community can be investigated; (2) to see if two or more communities differ; and (3) to see if the community is changing over time.
Diversity has two components: variety of forms, and relative abundance. Ecological processes generate a true relative abundance distribution for a set of species in a particular place at a particular time. Ecological sampling of that community produces an observed distribution that is a function of two patterns: the true distribution in nature, and sampling artifacts. Sampling artifacts may include random deviations from the true distribution due to under-sampling, sampling bias in which the sampling method favors the capture of some species over others, and errors in data entry.
The data from community sampling usually takes a particular form. Imagine an example in which an investigator takes a litter/soil sample in a patch of forest, and extracts the ants and identifies them. The investigator can present the results as a species list. Now imagine that the investigator has taken two samples instead of one. Some species will be common to both samples, others will be unique to one or the other. These results can be presented as a matrix with two columns and as many rows as there are species in both samples combined. The presence of a species in a particular sample is indicated by a check mark. Data such as these are presence/absence data or incidence data. Alternatively, the investigator may choose to count the number of individuals of each species in each sample. The cells of the matrix would then contain abundance data rather than presence/absence data. Our investigator may take ten replicate samples in old growth forest and another ten in managed forest nearby. The species-by-sample matrix now has the columns, which are different samples, organized in two groups. Species-by-sample matrices such as these are the fundamental data structure for ecological sampling. Replicate samples are represented by columns and species are represented by rows (or vice versa). The cell contents may be presence/absence data, or they may be abundances. The replicate samples may have no particular order or grouping, or they may be stratified or grouped in various ways.
Some species will be common in the dataset, and others will be rare. Terminology for rare species will become important in some analyses. Singletons are species known from a single specimen, and doubletons are species known from two. Uniques are species that occur in only one sample (regardless of their abundance within the sample), and duplicates are species known from two samples.
The results of our Brown Creek samples are in this dataset, which you should download and import into a spreadsheet or other data analysis program. The file is a tab-delimited text file, which you should download as "text," not "source." For treatments 1-4, each row in the dataset is a single pitfall trap. For treatment 5, each row is one team's catch. Variables associated with each trap are:
Treatment: 1 = 300yr forest, even-aged douglas fir forest; 2 = 18yr postharvest, extremely dense douglas fir and hemlock saplings; 3 = 33yr postharvest, precommercially thinned douglas fir forest; 4 = roadside through above three forest types; 5 = hand-collected specimens from half hour intensive search in river terrace area, mixed oldgrowth forest of conifers and deciduous trees, near river edge.
Team: teams of researchers, numbered 1-10.
Trap number: 1-10 for each treatment-team combination (0 for treatment 5).
Species 1, species 2, etc.: abundances of species in the trap; see species codes.
NOTE: DUE TO LOW DENSITIES IN TREATMENTS 2 AND 3, AND SOME CONFUSION OVER WHICH IS WHICH, WE WILL COMBINE THESE TWO TREATMENTS IN THE ANALYSES BELOW.
Does beetle density differ between the oldgrowth (treatment 1) and secondgrowth (treatments 2, 3) forests? The dependent variable is number of beetles in a trap (summed across species). The independent variable is forest type (oldgrowth vs. secondgrowth). n=100 for oldgrowth, 200 for secondgrowth.
TASK 1. Make two histograms, one for each forest type, showing the distribution of the dependent variable. Make each histogram the same size, and with proportional frequency on the vertical axis, so that they can be easily compared. What do you conclude from visual inspection of these graphs? State a null hypothesis you would use to examine differences among the treatments. What statistical test would you use to test for differences? If you have experience with statistics and know how to carry out the test, do it.
Does beetle diversity vary among forest types? A common way to examine sample data is with a rank - log abundance plot. All the species in a sample are ranked from most abundant to least abundant. Each species has a rank, which is plotted on the horizontal axis, and an abundance, plotted on the vertical axis. The abundance is plotted as the log of the proportional abundance. The species march across the page, a parade of ever shorter soldiers. Two separate features of this parade are considered components of diversity: 1) the total length of the parade, meaning the number of species in the sample or species richness, and 2) the evenness in soldier height, meaning the general steepness of the slope going from most to least abundant species. More even distributions (shallower slope in rank abundance plots) are defined as more diverse.
TASK 2. Make separate rank-log abundance plots for oldgrowth forest, secondgrowth forest (treatments 2 and 3), and the oldgrowth riparian forest (treatment 5). Make each plot the same size, with the same axes. What do you conclude from visual inspection of these graphs?
Numerous measures of diversity somehow boil rank abundance data down to one number, being variously influenced by species richness, species evenness, or both. Common diversity measures are sample species richness, Alpha, the Shannon Index, the Simpson Index, and the Berger-Parker index. These measures vary in how they are influenced by the species abundance distribution. Species richness, a measure that ignores evenness all together, is strongly influenced by the often long tail of rare species. "Dominance" indices, such as the Simpson and Berger-Parker, are strongly influenced by the few most abundant species. The Shannon Index is influenced by both species richness and by the dominant species. Alpha is influenced by the species of intermediate abundance, and is relatively insensitive to the rarest and most abundant species.
Alpha is calculated by first estimating x from the iterative solution of
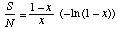
where S = the number of species in the sample and N = the number of individuals, and then calculating Alpha from
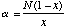
The Shannon Index is calculated as
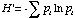
where pi is the proportion of individuals in the ith species.
Simpson's Index is calculated as
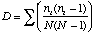
where ni is the number of individuals in the ith species. The higher D the lower the diversity, so the reciprocal of D is often used so that a higher number means higher diversity.
The Berger-Parker Index is calculated as
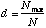
where Nmax = the number of individuals in the most abundant species. Like Simpson's index, higher d means lower diversity, so the reciprocal is often used.
TASK 3. Calculate species richness, Shannon index, reciprocal Simpsons index, and reciprocal Berger-Parker index for oldgrowth (treatment 1) and secondgrowth (treatments 2 and 3 together) (advanced work: do Alpha too).
TASK 4. What are some criticisms you might have of the methods and analyses employed, and what would you do differently to assess carabid density and diversity in the Brown Creek area?
Features of the biology of an organism may be revealed by their spatial distribution. A null hypothesis for spatial distribution is that individuals are randomly distributed with respect to each other. When the mean number of individuals per sampling unit is small, the expected distribution of individuals in sample units is approximated by the Poisson distribution. Deviations from a Poisson may be toward over-dispersion, in which individuals are too evenly distributed, or toward clumping, in which too many samples are empty and too many have relatively larger numbers of individuals.
TASK 5. Do Scaphinotus angusticollis from treatment 1 appear over-dispersed or clumped? Do they deviate significantly from a Poisson distribution?
John T. Longino, The Evergreen State College, Olympia WA 98505 USA. longinoj@elwha.evergreen.edu
Last modified: 20 October 1998