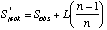
I am posting two data sets. The first one is a condensed format dataset that we will use for this assignment. The complete dataset is described at the end of this document.
In the condensed format dataset, the sample unit is a transect-day. There are a total of 86 transect-days. In 1992 transects A-G were sampled once each week for the first 7 weeks of the quarter. In 1994 transects A-G were sampled one time during week 2 of the quarter. In 1998 transects A-H,J,K were sampled on three consecutive days during week 2 of the quarter.
Structure of the dataset: transects are columns, species are rows. The first column contains variable labels. Row 1 is the year. Row 2 is the time period. Row 3 is the transect. Rows 4-31 are the abundances of 28 species. See the bottom of this document for the table of species codes, and link to the TESC Biota pages where the species are described.
Task 1. For each transect day, calculate total abundance, species richness, and Berger-Parker index. Examine the distributions of these variables. How has density, species richness, and evenness varied over the course of sampling? Plot these variables as a function of time period, over the 11 time periods from period 1 of 1992 to period 3 of 1998. Use your observations of the distributions of these variables to determine whether to use a log scale.
Task 2. Produce rank-log abundance plots for each year. How do they compare? Do carabids on the TESC campus exhibit a geometric distribution? Log series? Lognormal? Based on your results from tasks 1 and 2, does it look like carabid diversity is changing on campus?
Notes on species accumulation curves:
What is the rate of species accumulation in a sampling program? This question alone has no pretensions of describing community characteristics (although it can be applied to estimating community species richness; see below). The question has relevance to what is called "strict inventory," in which a goal is getting the largest possible species list for the least effort. Strict inventory is practiced by taxonomists who wish to efficiently sample many taxa for museum study.
The rate of species accumulation is observed with a species accumulation curve. A species accumulation curve has some measure of effort, usually number of samples, on the horizontal axis, and cumulative number of species on the vertical axis. A particular ordering of samples produces a particular species accumulation curve. The last point on the curve will be the total number of species observed among all the samples. Changing the order of samples may change the shape of the curve, but not the endpoint. A smoothed or average species accumulation curve can be produced by repeatedly randomizing sample order, calculating a species accumulation curve for each randomization, and averaging the resultant curves. The curve for a highly undersampled fauna will be nearly linear, with each new sample adding many new species to the inventory. The curve for a thoroughly sampled fauna will reach a plateau, with few or no species being added with additional sampling.
Rob Colwell, a community ecologist at the University of Connecticut, has developed a powerful tool for the analysis of ecological data. The program is called EstimateS (the link will take you to Colwell's Web site, which has the manual on-line), and we will use it to analyze our carabid data from the TESC campus.
Task 3. Use EstimateS to make separate species accumulation curves for each year. How do the curves compare?
Notes on estimating species richness:
Conservation biologists and environmental planners may be called upon to evaluate or rank different sites for their conservation value, and to monitor changes in conservation value over time. Although not the sole criterion in conservation value, community species richness is often considered one of the most important. Thus, obtaining reliable estimates of species richness is an important goal.
Biological communities are not precisely defined, and so the richness of a community cannot be either. Often sampling is area based (quadrats, sampling distributed along transects, etc.) and so as sample size increases the area sampled does too. Ultimately this is a species-area phenomenon, and one expects species richness to be an ever increasing function of sample area. However, it may be appropriate to treat communities as though they were discrete, with biodiversity partitioned into two parts: the species richness of local communities, and the complementarity - the dissimilarity - among these communities. This approach assumes that communities are like an urn with balls of different colors, and the task is to estimate the number of colors. When discrete, bounded communities are assumed, species accumulation curves rise due to undersampling, not due to species-area effects, and species richness is a finite community parameter.
There are three general methods of estimating species richness: extrapolating species accumulation curves, fitting parametric models of relative abundance, and using non-parametric estimators. Species accumulation curves can be fit to equations that contain an asymptote, and the asymptote becomes the estimated species richness of the community. A difficulty with fitting asymptotic curves is that there are many different asymptotic equations, and multiple methods of fitting curves to them. This results in a plethora of different estimated richness values for the same observed species accumulation curve. Which of the different equations or curve-fitting methods is best is the subject of current investigation.
An oft cited richness estimation procedure is to fit relative abundance data to a lognormal curve, and then estimate the area under the "hidden" portion of the curve. Problems of fitting a continuous distribution to discrete data and the lack of a method for calculating confidence intervals for the estimates recommend against its use in most cases.
Some non-parametric methods show the greatest promise for richness estimation. These methods have been developed for the general problem of taking a sample of classifiable objects and estimating the true number of classes in the population. In ecology, such methods have been most frequently applied to estimating population size from mark recapture data. Estimating richness is essentially the same problem, with the abundance of a species in a sample equivalent to the number of captures of an individual in a mark recapture study.
A commonly used non-parametric estimator is the first-order jackknife. The estimate of species richness is based on the number of uniques (L, species occurring in one sample):
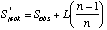
where Sobs is the observed number of species, and n is the number of samples.
Another non-parametric estimator that shows considerable promise is Chao2:
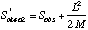
where L is the number of uniques and M is the number of duplicates (Chao's original formulation was for singletons and doublets, rather than uniques and duplicates). Colwell's manual to EstimateS discusses the new coverage-based estimators that Chao and colleagues have developed, called ACE and ICE. These are extensions of the Chao1 and Chao2 estimators, incorporating data from additional abundance classes beyond the singletons and doubletons.
A desirable attribute of a richness estimator is that it be independent of sample size. Pielou's pooled quadrat method is a powerful means of evaluating the stability of a richness estimator (or any index of diversity) and its relationship to sample size. To use the method, first randomize the sample order. Calculate the richness estimate based on the first sample, then on the first two samples pooled, then on the first three samples pooled, and so forth. Plot the estimate as a function of number of pooled samples. A well-behaved estimator will level-off, even as sample size is increasing. Just as a raw species accumulation curve can be smoothed by repeatedly randomizing sample order and averaging the curves, the estimate curve can be the average of many randomized sample orders.
Task 4. Examine the ACE richness estimate curves. How do they behave, and how do they compare among years? Examine the behavior of Fisher's Alpha, the Shannon Index, and Simpson's Index as a function of sample size. If we want to characterize community diversity of the TESC carabids using these diversity indices, what are appropriate sample sizes?
Task 5. Pick a question you want to examine using this dataset. State the question and carry out the analysis.
Link to Complete Dataset.
Complete Dataset Structure:
Each row is a single pitfall trap for one day. Row 1 contains variable labels.
The variables are:
For the following variables, each is a species, with values = number of individuals of that species in trap. Details about these species may be found at the Evergreen Biota website.
John T. Longino, The Evergreen State College, Olympia WA 98505 USA. longinoj@elwha.evergreen.edu
Last modified: 29 October 1998