K+ (g) + e- ® K (g) DH = -IE = -418.8 kJ/mol
Cl- (g) ® Cl (g) + e-
DH = -(-EA) = 349.9 kJ/mol
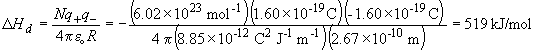
So, DH1 = DHd -IE + EA = 519.0 -418.8 + 349.9 = 450.1 kJ/mol
Spring Chemistry Homework #6 Answer Key
Chemical Bonding: The Classical Description
Oxtoby, Nachtrieb and Gillis: Chapter 3
11. This is a Hess's Law problem. The reaction of interest is:
K+Cl- (s) ® K (g) + Cl (g) DH1 = ?This can be viewed as the sum of the following reactions:
K+ (g) + e- ® K (g) DH = -IE = -418.8 kJ/mol
Cl- (g) ® Cl (g) + e-
DH = -(-EA) = 349.9 kJ/mol
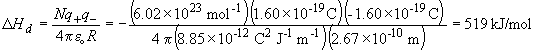
So, DH1 = DHd -IE + EA = 519.0 -418.8 + 349.9 = 450.1 kJ/mol
23. The Lewis structure for urea is:
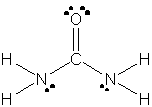
The bond lengths are estimated to be:
N-C: 1.47 Å
N-H: 1.01 Å
C=O: 1.20 Å
26.
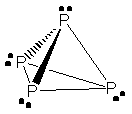
28.
a) HNC
Formal Charges: H: 0, N: +1, C: -1

According to the Electroneutrality Principle, the middle resonance form is the most stable since it minimizes the number of formal charges and has the negative charge on the most electronegative element.
c) H2CNN
There are no other resonance structures that satisfy the octet rule for both nitrogens and carbon. The formal charges are: C: 0, H: 0, Ncentral: +1, Nterminal: -1.
Chapter 19: Lattice Energies
33. The lattice energy, U, for LiF is the equal to the enthalpy change of the following reaction:
Li+(g) + F-(g) LiF (s) DH = UThis can be viewed as one step in the overall formation of LiF.
Li (s) ® Li (g) DH = DHºf (Li) = 159.4
½ F2 (g) ® F (g) DH = DHºf (F) = 79.0
Li (g) ® Li+(g) + e- DH = IELi = 520.2
F (g) + e- ® F- (g) DH = -EAF = -328.0
Li+(g) + F-(g) ® LiF (s) DH = U
__________________ _____________________
Li + ½ F2 (g) ® LiF (s) DH = DHºf (LiF) = -616.0
By Hess's Law: DHºf (LiF) = DHºf (Li) + DHºf (F) + IELi - EAF + U
Rearranging,
-U = DHºf (Li) + DHºf (F) + IELi - EAF - DHºf (LiF)
-U = 159.4 + 79.0 + 520.2 -328.0 -(-616.0)
U = -1,046.6 kJ/mol
b) Calculating the lattice energy using the Born-Lande equation yields:
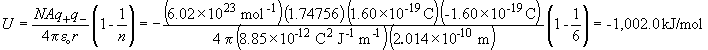
So the calculated value is within about 4% of the experimentally observed lattice energy. Note that A is the geometric factor for the rock salt structure and n is the compressibility factor provided in the question.
DeKock & Gray: Chapter 2
7. The electron configuration for all of these species is: 1s22s22p6. The order of atomic (or ionic) radii will be:
Na+ < Ne < F- < O2- < N3-
This is because the nuclear charge, which pulls the electrons toward the center of the atom, is decreasing from left to right. As a result, the attractive force between the electrons and the nucleus is decreasing, allowing the electrons to extend farther out in the more negatively charged species.11. This differs from question 11 above in that the products of the dissociation are ions instead of neutral atoms. The reaction of interest is then:
Li+F- (g) ® Li+ (g) + F- (g) DH = DHd\
The bond dissociation energy, DHd is given by:
18.
acetylene (C2H2) ethylene (C2H4)
The C-C bond in C2H2 should be both shorter and stronger than that of C2H4 because the former is a triple bond and the latter is only a double bond. Both molecules will be non-polar.22. The relevant Lewis structures are:
CN- and CO are isoelectronic in that they have equivalent electron structures. The C-O bond length is shorter in CO than in CO2 because it is a triple bond, meaning there are three electron pairs being shared by the two atoms.
Additional Lewis Structures:
a) FBr
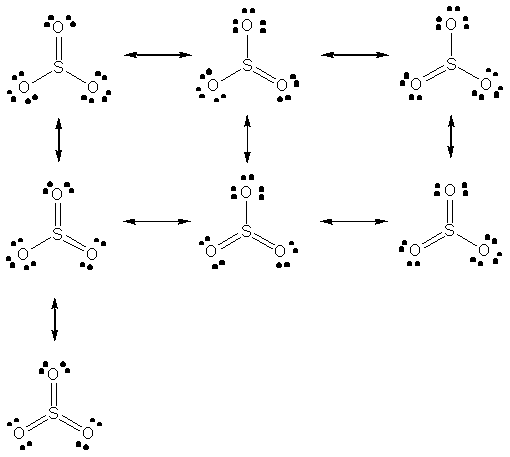
There are seven possible resonance forms for SO3. By formal charge considerations, the bottom structure (3 double bonds) is the most stable.
c) N2F2
d) NCO-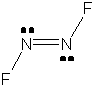
By formal charge considerations, the structure on the right is the
most stable resonance form.
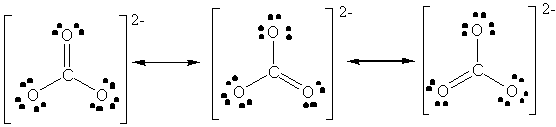
e) CO32- (carbonate). There are three equivalent resonance forms of carbonate:
f) CS2 (carbon disulfide)
![]()
The central resonance form is the most stable since there are no formal charges.
g) BF4- (tetrafluoroborate)