 A schematic of the model we used last week looked like Figure 4.1.
A schematic of the model we used last week looked like Figure 4.1. Mathematical Modeling
Solar Fluxes and the Earth's Atmosphere
Objectives The objectives of this lab are to study a simple model of planetary temperatures with atmospheres based upon energy flows.
Background The fundamental difference between this lab and the one you did last week, is that we now add an atmosphere to the planet. An atmosphere will affect the surface temperature of a planet, but will not affect the exterior temperature (the radiant temperature seen by an observer out in space) of the planet. The exterior radiant temperature is determined from equilibrium where the net solar inflow is equal to the IR radiated outflow. The net solar inflow is a function only of the solar flux and the planetary albedo.
 A schematic of the model we used last week looked like Figure 4.1.
A schematic of the model we used last week looked like Figure 4.1.
Figure 4.1
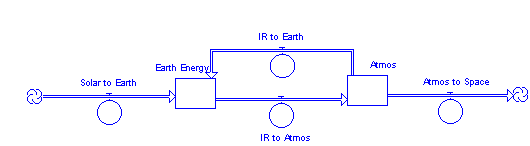 We now add an atmosphere that we assume (for simplicity) is transparent to visible light, but totally opaque to infrared radiation. Such an atmosphere absorbs all the IR radiated by the earth, and re-radiates it in all directions, half of it going back to the earth, and half of it going out into space. Such a model is schematically depicted in Figure 4.2.
We now add an atmosphere that we assume (for simplicity) is transparent to visible light, but totally opaque to infrared radiation. Such an atmosphere absorbs all the IR radiated by the earth, and re-radiates it in all directions, half of it going back to the earth, and half of it going out into space. Such a model is schematically depicted in Figure 4.2.
Figure 4.2
The atmosphere of Earth is, in fact, not totally opaque to IR radiated from the earth, but rather allows some of the IR to pass directly through. If we define fIR abs as the fraction of the IR radiated by the ground that is absorbed by the atmosphere, then (1 - fIR abs ) passes directly from the ground to space. A schematic for such a model is shown in Figure 4.3, at the top of the next page.
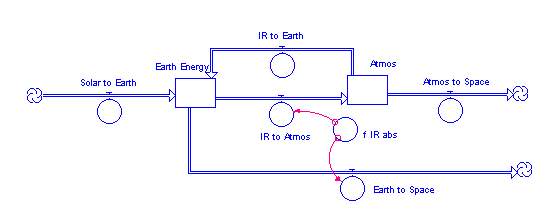
Figure 4.3
To explore such models, we will modify the model you constructed last week. Rather than compute heat capacities for water and for the atmosphere in the midst of the diagram, we'll separate them from the main schematic portion of the flows. Examine Figure 4.4 (on the next page) carefully, and then build a similar model, using your model from last week as a starting point. Use the initial values of zero for the Earth Energy and Atmosphere stocks, and all of the parameter values from last week. In addition, the following values will be necessary:
Atmos Depth 5600 { m }
Density Atmos 1.293 { kg / m^3 }
Specific Heat Atmos 1004 { J / (kg * K) }
Note that we are assuming that the atmosphere is of constant density, but only 5600 meters thick. This is an excellent approximation to our real atmosphere whose density decreases with height, and is actually much thicker.
After setting up a graph to plot T_grd and T_atmos, and Numerical Displays for each quantity, run a simulation with from time 0 to 1 with DT = 0.0025. Your temperature values should be the same as those show at the bottom of Figure 4.4.
The atmosphere temperature remains at 255 K, but the ground temperature is now 303 K, or
30 C, which is the same as 86 F. This is a bit warmer for an average earth temperature than actually exists, but recall that our starting assumption was that the atmosphere absorbed all the infrared radiation from the earth, and so half of that got radiated back to the earth to be reabsorbed. In actual fact, the atmosphere is transparent to some wavelengths of infrared radiation, and so less radiation that our model projects gets radiated back to the earth, and hence the actual surface temperature is lower than the 303 K our model suggests.
One of the concerns that climatologists have is that human activity (clearing of forests, building of industrial parks, strip malls and suburbs, is that this may be changing the surface albedo of the planet. Use this model to find the sensitivity of the surface temperature to albedo change. That is, find the percent change in the surface temperature if the albedo changes by 1%.
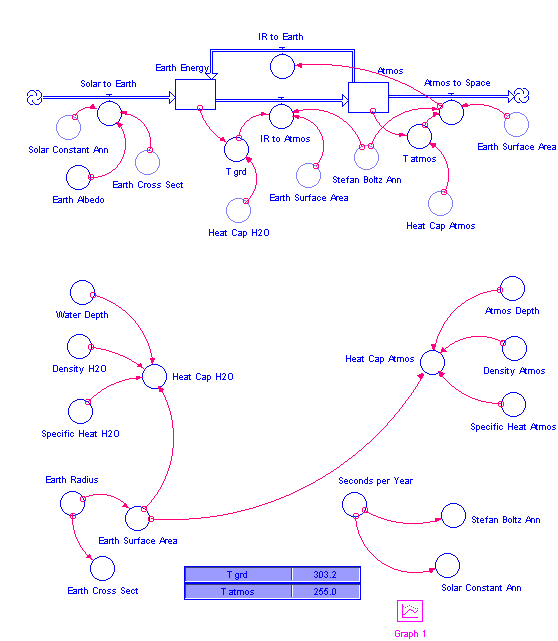 Figure 4.4
Figure 4.4
Now we will assume that the atmosphere absorbs only a fraction, fIR abs , of the IR radiated by the Earth. That means that ( 1 - fIR abs ) of the IR radiated by the Earth flows directly to space. Such a model is depicted on the next page.
Construct such a model (see the next page), and vary the value of fIR abs until you obtain an equilibrium surface temperature of 289.4 K, a value for the mean surface temperature of the Earth that is generally accepted by climatologists. What value for fIR abs did you obtain?
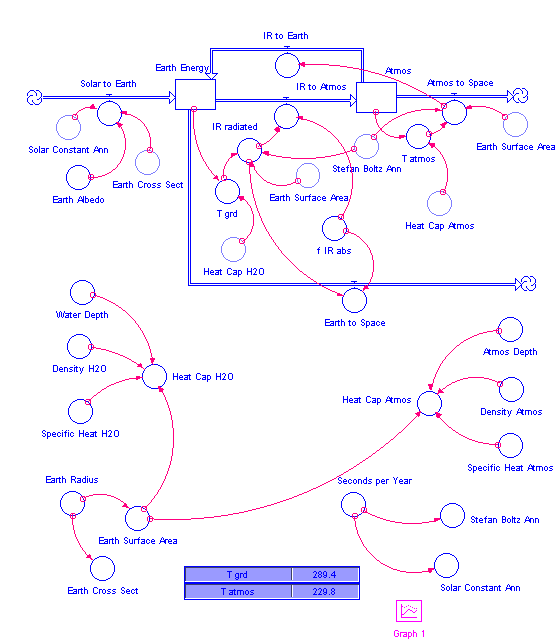 Figure 4.5
Figure 4.5
This model depicts the energy flow for the Earth with the assumption that the atmosphere absorbs only a fraction, fIR abs , of the IR radiated by the surface of the planet. When we vary
fIR abs such that the equilibrium surface is 289.4 K, then the equilibrium atmosphere temperature is just shy of 230 K. This is cooler than we observe on the Earth, but we have neglected the convective flow of heat and latent heat transfer from the surface to the atmosphere. Were we to include this as a next step, we would find the model predicts an equilibrium atmospheric temperature very close to that which climatologists believe is accurate. However, we've done enough with our model for this week.