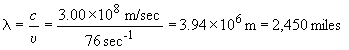
Problems from Kotz & Treichel
Chapter 7
23)
27)
| Wavelength | Spectral Region | energy per photon | energy per mol of photons |
| 285.2 | UV | 6.970 ´ 10-19 J | 420 kJ |
| 383.8 | UV | 5.179 ´ 10-19 J | 312 kJ |
| 518.4 | Visible | 3.834 ´ 10-19 J | 231 kJ |
31) In order of increasing energy per photon:
radio waves (radar) < microwaves < red < ultra-violet < g rays
33) For the device to work using the metal selected, there must be photons
present that have energy equal to or greater than 6.7 ´
10-19 J. The light available has a minimum wavelength of 540
nm. This corresponds to the following energy:
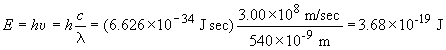
The device will not work since the available light cannot cause photoemission
of electrons from the metal surface. L
71) The total energy of the signal is equal to the sum of all of the photon energies present, or E = nhn, where n is the number of photons in the signal. Therefore,
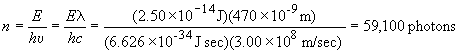
Additional Questions:
1)
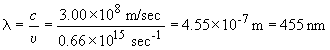
E = hn = 4.37 ´ 10-19J
2) To do this problem, you need to first find the total energy density,
u, by the relationship u = aT4,
where a = 7.566 ´
10-16 J m-3 K-4. You then need to calculate
the energy that is emitted in the visible region of the electromagnetic
spectrum. You can do this by plotting the function,
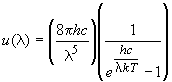
between 400 to 700 nm and estimating the area by a summation of rectangles,
i.e., determine the Riemann sum. By multiplying the height of each rectangle
(the value of u(l)), by the width Dl,
followed by summing these values will yield an estimate of the area. Note
that the function u(l) has units of J
m-4; using meters on the x-axis yields an area with units
J m-3, which is correct for energy density.
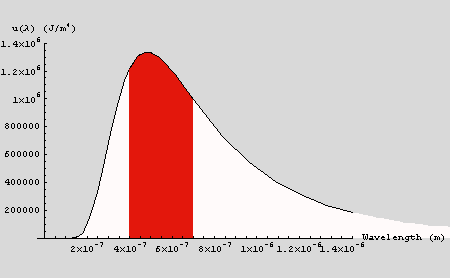
In the case of the sun (T = 6000 K), the above plot illustrates the
calculation. The total area under the curve is u. The shaded area
corresponds to the light that is in the visible portion of the spectrum;
the area of the shaded region can be estimated by the Riemann sum described
above. In this case, u = 0.9805 J m-3. The area between
400 and 700 nm is 0.37 J m-3. Thus 38% of the radiant energy
of the sun is in the visible portion of the spectrum. Results for the other
cases are summarized below. Note that as the objects get cooler, the total
energy density decreases as does the fraction of radiant energy in the
visible part of the spectrum.
| T (K) | Energy Density, u (J m-3) | Energy Density in the Visible Range (J m-3) | Percent of Energy in the Visible Range |
| 1000 | 7.566 ´ 10-4 | 1.1 ´ 10-9 | 1.4 ´ 10-4 % |
| 2500 | 2.955 ´ 10-2 | 9.1 ´ 10-4 | 3.1 % |
| 6000 | 0.9805 | 0.37 | 38 % |
3a)
b)