The average rate for each interval was calculated by the following equation:
![]()
The negative sign is included because the concentration provided is that of a reactant, that is, it is decreasing as the reaction progresses.
Review Assignment #5
Chapter 14 - Chemical Kinetics
5)
|
Time (s)
|
[CH3NC]
|
Average Rate*
|
|
0
|
0.0165
|
2.75E-06
|
|
2000
|
0.0110
|
1.70E-06
|
|
5000
|
0.00591
|
8.33E-07
|
|
8000
|
0.00341
|
5.10E-07
|
|
12000
|
0.00137
|
2.10E-07
|
|
15000
|
0.00074
|
10.
The average rate for each interval was calculated by the following equation:
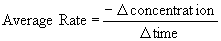
The negative sign is included because the concentration provided is that of a reactant, that is, it is decreasing as the reaction progresses.
|
a. |
|
|
b. |
|
|
c. |
|
16a. rate law: rate = k [N2O5]
b.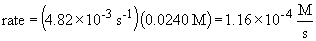
c. when the concentration of N2O5 is doubled, the rate doubles since it is a first order process. That is,
20a. rate law:
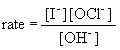
b. If the concentration of iodide is tripled, the rate will also triple.
c. If the concentration of hydroxide is doubled, the rate will drop by one-half.
22. To find the rate law, you first must determine
the order of the reaction with respect to each reactant. A comparison of
experiments 1 and 2 will give the order with respect to NH3
(since [BF3] is not varied). In these experiments, the ammonia
concentration is reduced by one-half and so is the reaction rate falls
by one half as a result. Since it is a proportional change, the reaction
must be first order in NH3. Or, more systematically, we can
say:
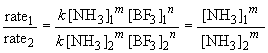
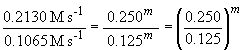
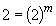
Thus m, the order of the reaction with respect to NH3, is equal to one.
Similarly, a comparison of the rates observed in experiments three and four will yield the order of the reaction in BF3 since the initial concentration of NH3 is the same in both cases. By the above procedure,
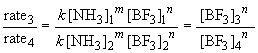
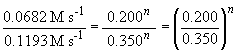
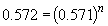
Thus n, the order of the reaction with respect to BF3, is equal to one.
So, the rate law is: rate = k [NH3] [BF3]. This reaction is second order overall (m + n =2).
The rate constant can be calculated from any one of the experiments. Using the data from experiment 1,

28. In this problem, it is important to realize that
pressure can be used in place of concentration in the integrated rate law
(because the ratio of pressures of time will be exactly equal to
the ratio of concentrations).
The appropriate equation is the first-order integrated rate equation:
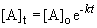
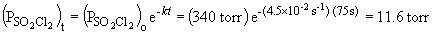
b) When the pressure is equal to one-tenth the initial pressure, we can set up the ratio,
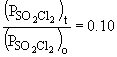
Rearranging the integrated rate equation, we can say,
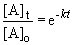
So,
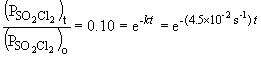
Taking the natural log of both sides:
35. To determine the order of this reaction, we need
to plot the concentration data two ways:
first order plot: ln [NO2] vs. tsecond order plot: 1/[NO2] vs. t
The plot that gives the strait line indicates the order of the reaction. The plots are shown below.
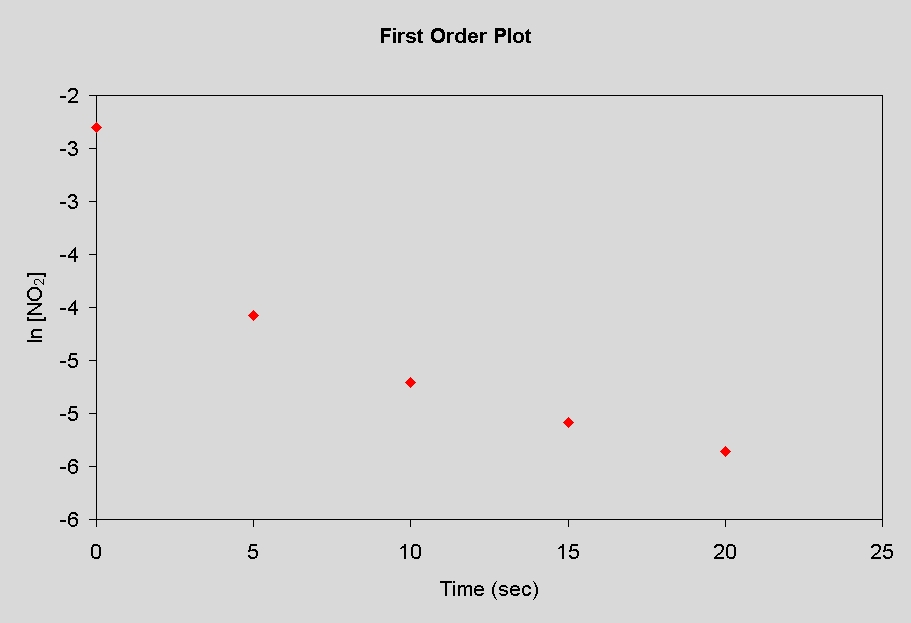
Since the second order plot is linear, the reaction follows second order kinetics. With this type of plot, the rate constant is equal to the slope. So, the rate constant is 10.2 M-1 sec-1.
42. The energy profile for this reaction is similar
to what is shown in Figure 14.15, although the relative size of Ea
and DE are not the same. The activation energy
of the reverse reaction will be 73 kJ.
47. Here's that damn question I messed up in lecture. Let's try it one more time. We can set up a ratio as follows:
a)
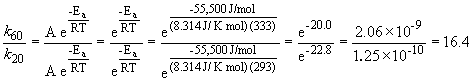

k60 = 2.88 s-1
b)
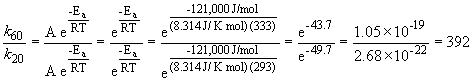

k60 = 68.6 s-1
56. Since each of these are elementary processes the
rate laws can be determined from the balanced equations:
a) bimolecular, rate = k [CH2] [Cl2]60. Mechanisms b and d are both consistent with the observed rate law.
b) unimolecular, rate = k [C3H6]
c) unimolecular, rate = k [SO3]
74. Comparing experiments 1 and 2:
75 a. The rate law is: rate = k [NH2CONH2]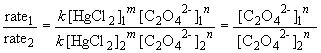
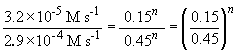
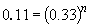
Thus, n = 2.
Comparing experiments 1 and 4 yields:

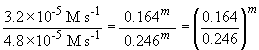
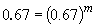
So, m = 1. The rate law is then: rate = k [HgCl2] [C2O42-]2
b) The rate constant is (using data from experiment 1)
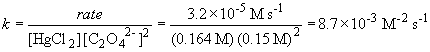
c)
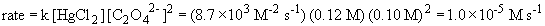
79. The rate law will be: rate = k [H2O2] [I-]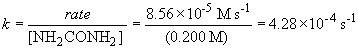
b. [A]t = [A]oe-kt
[A]t = (0.500 M)e-(4.28 ´ 10-4 s-1) (5 ´ 103 s) = 0.059 M
The overall reaction is: 2 H2O2 (aq) ® 2 H2O (l) + O2 (g)IO- is the intermediate in this mechanism.