Introduction

Species diversity (sometimes called species heterogeneity) is an expression of community structure. A community is said to have high species diversity if many equally or nearly equally abundant species are present. Conversely, if a community is composed of a very few species, or if only a few species are abundant, then species diversity is low. For example, if a community had 100 individuals distributed among 10 species, then the maximum possible diversity would occur if there were 10 individuals in each of the 10 species. The minimum possible diversity would occur if there were 91 individuals belonging to one species and only one individual in each of the other nine species.

High species diversity indicates a highly complex community, for a greater variety of species allows for a larger array of species interactions. Thus, population interactions involving energy transfer (food webs), predation, competition, and niche apportionment are theoretically more complex and varied in a community of high species diversity. There is general agreement among ecologists that high species diversity is correlated with community stability; the ability of community structure to be unaffected by disturbance of its components. However, a few maintain that there is no simple relationship between diversity and stability.

Objectives

The objectives of this exercise are to:

• To introduce you to two of the most popular species diversity indices; Simpson's Index, and Shannon's Index,
• Gain expertise in computing species diversity indices from a real data set and interpret the results

Simpson Index

A good measure of diversity should take into account both the number of species and the evenness of occurrence of individuals in the various species. Simpson's Index (1949) considered not only the number of species (s) and the total number of individuals (N), but also the proportion of the total that occurs in each species. This diversity index is an expression of the number of times one would have to take pairs of individuals at random from the entire aggregation to find a pair from the same species. This diversity index is the inverse of Simpson's dominance index and is expressed as:

where:

D_s = Simpson's Index of Diversity

N = total number of individuals of all species

n_i = total number of individuals of a species

Table 1: Hypothetical species abundance data used to illustrate the calculation of various diversity indices.

Species (i) Frequency (n_i) Relative Abundance (p_i)

= 1 - 3140/7140 = 1 - 0.439 = 0.56

Simpson’s Index is the probability that any two individuals, chosen randomly from the same site, would be different species. As diversity increases, D_s increases.

Shannon Index

The Shannon Index is another widely employed species diversity index. Derived from information theory, it measures the degree of uncertainty in a sampling event. That is, if diversity is low, then the certainty of picking a particular species is high. If diversity is high, then it is difficult to predict the identity of a randomly picked individual. The mathematical expression of the Shannon Diversity Index is shown below:

H = (N log N - ·n_i log n_i) /N

where:

H = the Shannon Index of Diversity

Example 2: Using the data in Table 1 as an example for calculating the Shannon Index yields:

H = [85 log 85 - (50 log 50 + 25 log 25 + 10 log 10)] /85

= [164.001 - (84.949 + 34.949 + 10.000)]/85 = 34.103/85 = 0.40

The Shannon Index (H) is appropriate when you have a random sample of species abundance's from a larger community or sub-community of interest. Such a sample (unless extremely large) may not contain representatives for each species in the entire community. However, the lack of data on rare species has little effect on the value of H.

Exercise

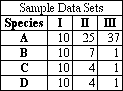Calculate Simpson’s and Shannon’s Indices for the data given below.

Q1. How do the two indices vary between the sites? Do they both give you the same information?

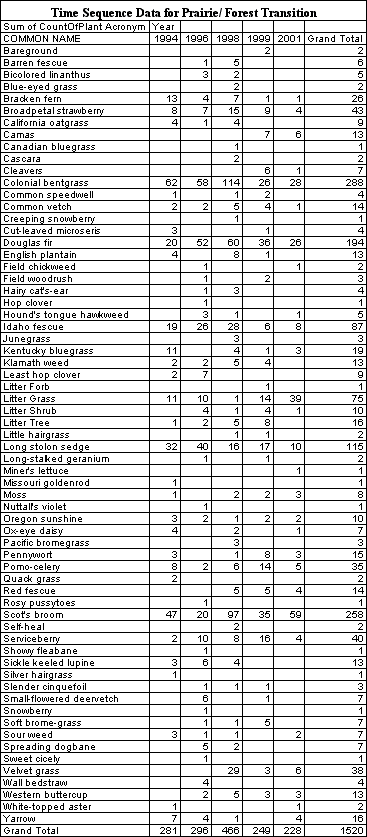
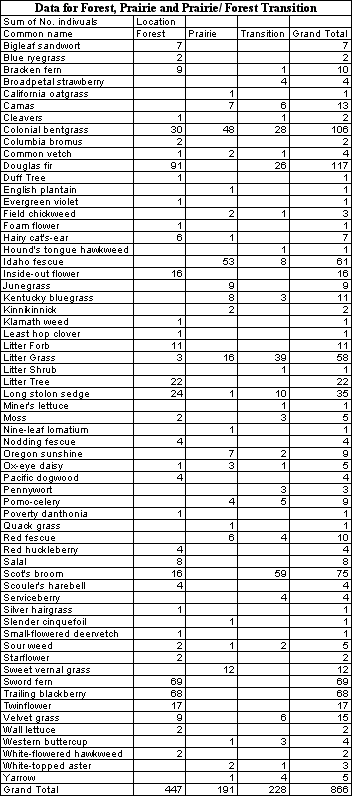
Q2. Calculate Simpson’s Index for one of the data sets given out in class. Compare the relative diversity of the sites. There are two data sets, both from Fort Lewis. The first data are from a plot in a transition zone between prairie and forest that was sampled over a period of years. The second data are from three different sites, a prairie, a transition between prairie and forest, and a forest site. Make a statement about the relative diversity of the sites your group analyzes.