A Proof of the Pythagorean Theorem
The Physicist's World
A Proof of the Pythagorean Theorem
Introduction
The following proof of the Pythagorean theorem is an adaptation of
a proof given in From Pythagoras to Einstein
by K. O. Friedrichs, Chapter 1. The proof uses geometric intuition and
approach, however, it relies on a modern algebraic interpretation of geometric
objects. Figure 1 depicts the theorem to be proved. The quadrilaterals
labeled A, B, and C in the figure denote areas and we want to show
that A + B = C by areas. Using modern algebraic techniques, we know
that the areas of A, B, and C are, respectively, a*a, b*b, and c*c,
where a, b, and c denote lengths. It is common to
refer to the square A, or the side a, however, one must remember that
strictly speaking A denotes an area and is not a name for the quadrilateral
and similarly, "a" denotes a length and is not a name for the side.
Traditional Euclidean geometry until the time of
Descartes (c. 1630) identified geometric entities as magnitudes and
referred to them by name, such as a list of names of corner points for
a square. They did not allow "non-homogeneous" mixing of magnitudes of
different dimensions. For example, magnitude a*a was a product of
linear magnitudes, resulting in a linear magnitude which could
never equal the magnitude of a planar object. Consequently, denoting
the area of the square A by a*a would make no sense.
Assumptions
The following propositions are assumed in the proof below.
A proof relies on commonly agreed upon truths and the most significant
assumptions are usually stated. Typically many "obvious" assumptions are not
stated.
- In a right triangle, one angle is a right angle and the other two
angles sum to a right angle.
- Two right angles combine to form a straight line, and cannot combine
to form any other angle.
- If three angles combine to a straight line and two of the three
angles sum to a right angle, then the third angle must be a right angle.
(Follows from assumptions 1 and 2)
- A quadrilateral is a rectangle if the corners are right angles.
- A rectangle is a square if the sides are all equal in length.
- The area of a rectangle with sides of length a and b is a*b.
- The area of a square with sides of length a is a*a
- The area of a triangle with base b and height a is (a*b)/2.
Proof of the Pythagorean Theorem
Figure 1 depicts the theorem to be proved. We must show that the area A
plus the area B equals the area C.
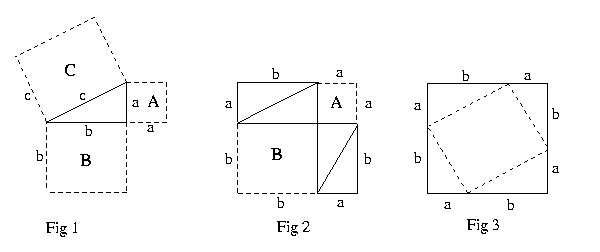
- Construct the square in Figure 2. First arrange the squares A and B
so that the adjoining corners of A and B form four right angles. Next
complete the larger square by extending the outer edges. The larger square
consists of the squares A and B plus two rectangles each with sides a and b.
The total area of the larger square can be described in two ways.
(1) (a+b)*(a+b)
(2) a*a + b*b + 2*a*b
- Construct the square in Figure 3. Arrange four triangles each with sides a
and b to adjoin at corners with the long leg (length b) to the left of the
short leg and with the outer adjoined edges lined up straight to form a
quadrilateral. The large quadrilateral is a square because the four corners
are all right angles and the sides all have the same length (a+b). The
enclosed area shown by the dotted lines forms a square with sides of length
c. To see this, first consider the corners of the enclosed area which
coincide with the points on the side of the larger square where the triangles
adjoin to form three angles. The inner angle must be a right angle because
the other two angles sum to a right angle and all three angles combine to a
straight line (see assumptions 1,2,3 above). The sides of the enclosed
area are evidently length c, the length of the hypotenuse of the enclosing
triangles with sides a and b. The total area of the larger square in Figure 3
can be described in two ways.
(3) (a+b)*(a+b)
(4) c*c + 2*a*b
- The area formulas for figures 2 and 3 can are equal, because they
are both (a+b)*(a+b) from (1) and (3) above. According to the alternate
formulas (2) and (4) for areas of
figures 2 and 3, we obtain the following equality of areas:
(5) a*a + b*b + 2*a*b = c*c + 2*a*b
(6) a*a + b*b = c*c (by subtracting 2*a*b from both sides of the equation)
Equation (6) is the result to be proved.

