The purpose of this workshop is to create and present a mathematical proof for the Pythagorean Theorem. You are guided through the ideas behind the construction of a particular proof by a series of questions. Answer all the questions in the workshop and then see if you can organize your knowledge into a written demonstration in the form that you learned in the previous Demonstrative Euclidean Geometry workshop.

General directions

1. Divide into groups of three or four. Produce one writeup with all group member names listed at the top.
2. Take each section at a time and try to answer all of the questions, but move on if you get stuck.
3. Observe the specified time limits as well as you can.
4. Prepare to present your demonstration to the rest of the class.

Exercise 1 - The Pythagorean theorem (20 minutes)

1. State the Pythagorean theorem as you recall it in English.
2. State the Pythagorean theorem in symbols and pictures.
3. Read the attached handout about Socrates' discussion of geometry in the Meno. Make sure everyone in the group understands the geometric construction and the associated argument that the construction is correct.
4. We say two two triangles are equal or, in geometry, congruent if they can be made to coincide, that is, if all of the sides precisely correspond. Give an argument demonstrating that two right triangles must be congruent if the two sides of the right angle are equal. Note: From the previous workshop, postulate 10: "One and only one perpendicular can be erected to a given line at a give point on the line".

Exercise 2 - Triangles and angles (10 minutes)

1. How many degrees in a full circle?
2. How many degrees in a half circle?
3. What is a right triangle? Draw one.
4. How many degrees in a right angle?
5. How many degrees in the sum of the angles in a square? a rectangle?
6. What is the definition of a square?
7. How many degrees in the sum of the angles in a right triangle?
8. How many degrees in the sum of the two angles opposite the right angle in a right triangle.

Exercise 3 - Area of rectangles and right triangles (10 minutes)

1. What is the expression for the area of a rectangle with sides of length a and b. Draw a picture of your rectangle and write down your area expression.
2. Show how to divide any rectangle up into two right triangles of equal area. Explain how you know they are equal in area.
3. What is the area of a right triangle with hypotenuse c and sides a and b? Draw a picture of your right triangle and write down your area expression.
4. What is the expression for area of each of the three squares A, B, and C in Figure 1? The labels on the edges represent the length measure of that edge.

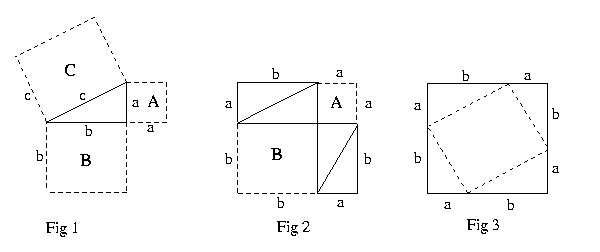
Exercise 4 - Proof of the Pythagorean Theorem (20 minutes)

1. Label the four triangles in Figure 3 to show how they correspond to the the triangles of Figure 2.
2. Using your knowledge from Exercise 2 above, make an argument that the inner bounded area in Figure 3 is indeed a square. You can't rely on the picture alone as justification because pictures can be misleading.
3. Is the sum of the areas of the four right triangles in Figure 2 the same as the sum of the areas of the four right triangles in Figure 3?
4. What is the area of the largest outer rectangle in Figure 2? What is the area of the largest outer rectangle in Figure 3? Are they the same?
5. What are the areas of the squares A, B, and C in Figures 2 and 3?
6. Give the expression for the area of the large outer square in Figure 2 minus the area of the four right triangles?
7. Give the expression for the area of the large outer square in Figure 3 minus the area of the four right triangles?
8. What can we conclude about the relationship of the areas calculated in parts 6 & 7 given the areas calculated in 3, 4, and 5?

Exercise 5 - Demonstration of the Pythagorean Theorem (20 min)

You will need to organize the proof section of your demonstration as you did in the Demonstrative Geometry workshop, but your justifications for each step of the proof need not be as formal in referencing specific axioms and propositions. Your reasons for each step should be clear, precise, and persuasive to the reader based on what you know and believe from the previous exercises in this workshop.