A. Make an estimate for each
question below. B. Explain your reasoning. C. Estimate the
uncertainty in your guess. Could it be twice as big? 100 times
smaller? More?
(1) What fraction of the stars in our galaxy are similar
to the Sun? S=____
(1.b) Reason:
(1.c) Uncertainty?
(2) What fraction of those sun-like stars might have planets?
fp = ____
(2.b) Reason:
(2.c) Uncertainty?
(3) How many "earths" would the average planetary
system have? Ne = ____
(3.b) Reason:
(3.c) Uncertainty?
(4) On what fraction of those earth-like planets would life
develop? fl = _____
(4.b) Reason:
(4.c) Uncertainty?
(5) On what fraction of those planets with life would the
life develop intelligence? fi = ____
(5.b) Reason:
(5.c) Uncertainty?
(6) On what fraction of those planets with intelligent life
would technology develop? fc = ____
(6.b) Reason:
(6.c) Uncertainty?
(7) Estimate the fraction of the planet's lifetime during
which the average communicating civilization survives: civilization's
lifetime ____ / planet's lifetime ____ = ______ = L
(7.b) Reason:
(7.c) Uncertainty?
Discuss your estimates with your teammates. You need
not agree, but you should note the range of estimates
and their justifications.
D. Combine your guesses to estimate the number of communicative
civilizations in our galaxy. First get back together
with the whole class. One team will share its data at the
board, and Zita will demonstrate how to easily calculate an
order-of-magnitude estimate using scientific notation. Then
you will practice the method with your own data.
1. The fraction of stars in our galaxy with communicative civilizations
= x = S* Fp * Ne * Fl * Fi * Fc * L
How many stars would there have to be in our galaxy
for there to be at least one communicating civilization? (Hint:
invert x. Why?)
2. If there are 100 billion stars in the Milky
Way, how many communicating civilizations would there be? Call
this N.
E. Calculate the uncertainty in your estimate. The fractional
uncertainty in N is equal to the sum of the fractional uncertainties
in each factor. (Fractional uncertainties are unitless.)
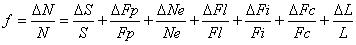
Then you can find the total uncertainty dN = N * f , which
has units of number of civilizations.
F. Now consider how much precision it is reasonable to retain
in your estimate for N. Write your estimate +/- uncertainty:
N +/- dN = _______ +/- ________
Your uncertainty dN tells you how many decimal places you can
reasonably keep in your N. For example, if you find N = 14.72836
and dN = 2, then you know N only to whole number precision:
N = 15 +/- 2.
Keep this in mind when you calculate in the future. Often in
astronomy, our data is quite approximate, so even if your calculator
gives you many decimal places, most of them are not significant.
Retain only significant figures, and do not waste your time
on meaningless precision. Order of magnitude estimates are often
the best we can do, and they can be quite interesting and useful.
As you develop your skill in making order-of-magnitude estimates,
you can impress your friends with back-of-the envelope calculations
G. Reflect on the meaning and consequences of your calculation.
Can we expect to hear from ET? How certain are you of your answer?
Are there other factors you might want to take into consideration?