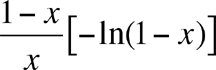
The purpose of this series of labs is to learn how ecologists define and measure diversity, and also to gain experience working with real insect samples from a tropical rainforest. The main references I have used to develop this exercise are Colwell and Coddington (1994), Gotelli and Colwell (2002), Longino (2000), Ludwig and Reynolds (1988), Magurran (1988), and Pielou (1975). A case study using many of these methods is Longino et al. (2002). The exercise has two main components:
(1) We will learn data manipulation and analysis techniques by working with a provided dataset. The data are from 16 samples of rainforest leaflitter ants.
(2) We will prepare and identify rainforest ants from a set of samples.
You will need to bring two pairs of forceps and a pair of scissors to lab. Also, a calculator will be handy at various times.
Ecologists and conservation biologists may want to measure diversity for a number of reasons: (1) to characterize the community so that the ecological and evolutionary processes generating the community can be investigated; (2) to see if two or more communities differ; and (3) to see if the community is changing over time.
Diversity has two components: variety of forms, and relative abundance. Ecological processes generate a true relative abundance distribution for a set of species in a particular place at a particular time. Ecological sampling of that community produces an observed distribution that is a function of two patterns: the true distribution in nature, and sampling artifacts. Sampling artifacts may include random deviations from the true distribution due to under-sampling, and sampling bias in which the sampling method favors the capture of some species over others.
The data from community sampling usually take a particular form. Imagine an example in which an investigator takes a litter/soil sample in a patch of forest, and extracts the ants and identifies them. The investigator can present the results as a species list. Now imagine that the investigator has taken two samples instead of one. Some species will be common to both samples, others will be unique to one or the other. These results can be presented as a matrix with two columns and as many rows as there are species in both samples combined. The presence of a species in a particular sample is indicated by a check mark. Data such as these are presence/absence data or incidence data. Alternatively, the investigator may choose to count the number of individuals of each species in each sample. The cells of the matrix would then contain abundance data rather than presence/absence data. Our investigator may take ten replicate samples in old growth forest and another ten in managed forest nearby. The species-by-sample matrix now has the columns, which are different samples, organized in two groups. Species-by-sample matrices such as these are the fundamental data structure for ecological sampling. Replicate samples are represented by columns and species are represented by rows (or vice versa). The cell contents may be presence/absence data, or they may be abundances. The replicate samples may have no particular order or grouping, or they may be stratified or grouped in various ways.
For diverse communities, species-by-sample matrices can be very large, and filled mainly with zeros. A more compact representation of the data matrix contains a row of data for each non-zero cell of the matrix. Each row contains the variables: abundance, species (usually a system of species codes is used), replicate, and any classifying variables such as old-growth vs. second-growth.
Some species will be common in the dataset, and others will be rare. Terminology for rare species will become important in some of the analyses discussed below. Singletons are species known from a single specimen, and doublets are species known from two. Uniques are species that occur in only one sample (regardless of their abundance within the sample), and duplicates are species known from two samples.
The data set you will analyze is real, produced by an arthropod survey project in a lowland rainforest in Costa Rica (Project ALAS, see Longino and Colwell 1997). The rows are ant species; the columns are samples. Each sample is from a set of small soil/litter cores, taken from the perimeter of a 10m radius circle, and extracted in Berlese funnels. Sixteen samples are shown, 8 from old-growth forest and 8 from second-growth forest. The values in the table are the number of adult workers.
Click here to download an Excel file; click here to view the data (or download it as tab-delimited text embedded in an html document).
A common way to examine sample data is with a rank abundance plot. All the species in a sample are ranked from most abundant to least abundant. Each species has a rank, which is plotted on the horizontal axis, and an abundance, plotted on the vertical axis. The species line up across the page, from most abundant to least abundant. Two separate features of this line-up are considered components of diversity: 1) the total length of the line-up, meaning the number of species in the sample or species richness, and 2) the evenness in abundance, meaning the general steepness of the slope going from most to least abundant species. More even distributions (shallower slope in rank abundance plots) are defined as more diverse. Rank-abundance plots are usually plotted with abundance on a log scale. The evenly-spaced divisions on the vertical axis are 1, 10, 100, 1000, etc. individuals.
When comparing rank-abundance plots from different samples, it is best to have a common vertical axis. This is done by plotting log(proportional abundance). The divisions on the vertical axis, starting at the top and going down, are 1, 0.1, 0.01, 0.001, etc.
Numerous measures of diversity somehow boil rank abundance data down to one number, being variously influenced by species richness, species evenness, or both. Some of them are designed to estimate community parameters, but the assumptions for an unbiased estimate are so restrictive that they can rarely be used for that purpose. For example, the Shannon index assumes that individuals are sampled from an infinitely large population, and that all species are represented in the sample. Because diversity indices are typically strongly influenced by details of sampling methods and sample size, a diversity value for a single sample has little meaning. However, instead of estimating community parameters, diversity indices can be used to assess differences between groups of samples. This follows Taylor's dictum that diversity indices are only as good as their ability to discriminate among sets of samples (Taylor 1978). The index is no longer an estimate of a community parameter, but rather a summary variable calculated from a particular sample. For example, for the Berlese data, we may want to know if samples from old growth forest somehow differ from samples from second growth forest. We can calculate the value of a diversity index for each sample, and compare the sets of values using a t-test.
Common diversity measures are sample species richness, Alpha, the Shannon Index, the Simpson Index, and the Berger-Parker index. These measures vary in how they are influenced by the species abundance distribution. Species richness, a measure that ignores evenness all together, is strongly influenced by the often long tail of rare species. "Dominance" indices, such as the Simpson and Berger-Parker, are strongly influenced by the few most abundant species. The Shannon Index is influenced by both species richness and by the dominant species. Alpha is influenced by the species of intermediate abundance, and is relatively insensitive to the rarest and most abundant species.
Alpha is calculated by first estimating x from the iterative solution of
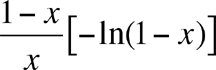
where S = the number of species in the sample and N = the number of individuals, and then calculating Alpha from
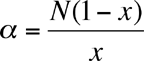
The Shannon Index is calculated as
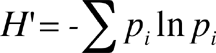
where pi is the proportion of individuals in the ith species.
Simpson's Index is calculated as
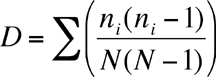
where ni is the number of individuals in the ith species. The higher D the lower the diversity, so the reciprocal of D is often used so that a higher number means higher diversity.
The Berger-Parker Index is calculated as
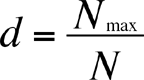
where Nmax = the number of individuals in the most abundant species. Like Simpson's index, higher d means lower diversity, so the reciprocal is often used.
When comparing diversity across some factor (habitats, seasons, time, methods) it is important to determine if there are major density differences. Two habitats may differ greatly in density but have similar numbers of species and similar relative abundance distributions. Within-sample diversity values for the low density site may be significantly lower than for the high density site, even though the actual diversity is the same. If there are large density differences, you may want to alter the definition of a sample replicate, such that it is based on a fixed number of individuals rather than a fixed area or amount of effort (Gotelli and Colwell 2001).
A decades long tradition has been to compare sample relative abundance data to mathematical distributions. Some of the distributions are based on particular biological models, others are "statistical' models judged purely on goodness of fit. Three of the most common distributions used to fit relative abundance data are the geometric series, the log series, and the log normal.
The geometric series predicts that in a rank-abundance plot each species abundance will be a constant proportion of the preceding species' abundance. If a log scale is used for abundance, the species fall along a straight line. In contrast, a log series or log normal distribution is non-linear. Geometric series distributions have lower evenness than log series or log normal. A biological mechanism which could produce a geometric series is the niche pre-emption hypothesis, in which the first species to arrive at a site monopolizes k percent of the available resources, the next species monopolizes k percent of the remaining resources, and so forth. Species-poor communities sometimes exhibit relative abundance distributions that fit a geometric series.
The log series predicts samples or communities dominated by a few very common species, similar to the geometric series, but also with many rare species. The preferred plot is a frequency histogram for which the horizontal axis is log(species abundance) and the vertical axis is number of species. The highest point of the distribution will always be the species known from singletons, with a steep monotonic decrease in numbers of species with higher abundances. The log series lacks an underlying biological model, but Alpha, one of the parameters of the log series distribution, has been touted as one of the best diversity indices.
The log normal predicts samples or communities in which most species are of intermediate abundance. There are fewer species that are either rare or very abundant. The preferred plot is the same as that used for the log series. The log normal distribution, as the name implies, forms a normal distribution instead of the monotonically decreasing distribution of a log series. However, if a community with a lognormal distribution is undersampled, only the rightmost part of the curve is revealed. As sampling increases, the "veil line" moves to the left, revealing more and more of the curve. With real sample data, if the mode of a log normal curve (the highest point in the distribution) is not revealed, it is practically impossible to distinguish from the log series.
A common tradition is to use log base 2, so that each abundance class represents a doubling of the previous one. In constructing observed distributions from real data, abundance classes are defined and the number of species in each abundance class tallied. Different methods have been proposed for defining abundance classes. A traditional way is to define abundance classes as 0-1, 1-2, 2-4, 4-8, 8-16, etc. For a species that stradles abundance classes (i.e., with abundance 1, 2, 4, 8, 16, etc.), 0.5 is added to the tally for each of the adjacent abundance classes. A problem with this method is that singletons are split between two abundance classes. The lowest abundance class will contain half the singletons, and the second lowest abundance class will contain half the singletons plus half the doubletons. This method forces the second lowest abundance class to have more species than the lowest, and thus gives the false impression that the mode of a log normal distribution has been revealed. The solution to this is to make the first abundance class the 1-2 class, with one half the singletons plus one half the doublets.
Magurran uses an alternative method of defining abundance classes. She defines the lowest abundance class as the sum of all the singletons and doubletons, the next lowest as species with abundance 3 or 4, next 5-8, 9-16, 17-32, etc. This method does not generate a "pseudo-mode" at the second abundance class. However it tends to inflate the size of the first abundance class, and is generally not used.
May (1975) has shown that the log normal distribution is common in the world, in both biological and non-biological applications (e.g., the distribution of wealth in the U.S.). The log normal distribution can be produced by combining the effects of many independent variables, each of which can have any underlying distribution. Thus, a log normal distribution of biological community data only reveals that many unknown and independent factors may be contributing to the observed community structure.
What is the rate of species accumulation in a sampling program? This question alone has no pretensions of describing community characteristics (although it can be applied to estimating community species richness; see below). The question has relevance to what is called "strict inventory," in which a goal is getting the largest possible species list for the least effort. Strict inventory is practiced by taxonomists who wish to efficiently sample many taxa for museum study.
The rate of species accumulation is observed with a species accumulation curve. A species accumulation curve has some measure of effort, usually number of samples, on the horizontal axis, and cumulative number of species on the vertical axis. A particular ordering of samples produces a particular species accumulation curve. The last point on the curve will be the total number of species observed among all the samples. Changing the order of samples may change the shape of the curve, but not the endpoint. A smoothed or average species accumulation curve can be produced by repeatedly randomizing sample order, calculating a species accumulation curve for each randomization, and averaging the resultant curves. The curve for a highly undersampled fauna will be nearly linear, with each new sample adding many new species to the inventory. The curve for a thoroughly sampled fauna will reach a plateau, with few or no species being added with additional sampling.
Conservation biologists and environmental planners may be called upon to evaluate or rank different sites for their conservation value, and to monitor changes in conservation value over time. Although not the sole criterion in conservation value, community species richness is often considered one of the most important. Thus, obtaining reliable estimates of species richness is an important goal.
Biological communities are not precisely defined, and so the richness of a community cannot be either. Often sampling is area based (quadrats, sampling distributed along transects, etc.) and so as sample size increases the area sampled does too. Ultimately this is a species-area phenomenon, and one expects species richness to be an ever increasing function of sample area (Rosenzweig 1995). However, it may be appropriate to treat communities as though they were discrete, with biodiversity partitioned into two parts: the species richness of local communities, and the complementarity - the dissimilarity - among these communities. This approach assumes that communities are like an urn with balls of different colors, and the task is to estimate the number of colors. When discrete, bounded communities are assumed, species accumulation curves rise due to undersampling, not due to species-area effects, and species richness is a finite community parameter.
There are three general methods of estimating species richness: extrapolating species accumulation curves, fitting parametric models of relative abundance, and using non-parametric estimators. Species accumulation curves can be fit to equations that contain an asymptote, and the asymptote becomes the estimated species richness of the community. A difficulty with fitting asymptotic curves is that there are many different asymptotic equations, and multiple methods of fitting curves to them. This results in a plethora of different estimated richness values for the same observed species accumulation curve. Which of the different equations or curve-fitting methods is best is the subject of current investigation.
An oft cited richness estimation procedure is to fit relative abundance data to a lognormal curve, and then estimate the area under the "hidden" portion of the curve. Problems of fitting a continuous distribution to discrete data and the lack of a method for calculating confidence intervals for the estimates recommend against its use in most cases.
Some non-parametric methods show promise for richness estimation. These methods have been developed for the general problem of taking a sample of classifiable objects and estimating the true number of classes in the population. In ecology, such methods have been most frequently applied to estimating population size from mark recapture data. Estimating richness is essentially the same problem, with the abundance of a species in a sample equivalent to the number of captures of an individual in a mark recapture study.
A commonly used non-parametric estimator is the first-order jackknife. The estimate of species richness is based on the number of uniques (L, species occurring in one sample):
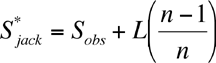
where Sobs is the observed number of species, and n is the number of samples.
Another non-parametric estimator that shows considerable promise is Chao2:
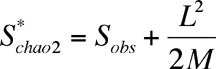
where L is the number of uniques and M is the number of duplicates (Chao's original formulation was for singletons and doublets, rather than uniques and duplicates).
A desirable attribute of a richness estimator is that it be independent of sample size. Pielou's pooled quadrat method is a powerful means of evaluating the stability of a richness estimator (or any index of diversity) and its relationship to sample size. To use the method, first randomize the sample order. Calculate the richness estimate based on the first sample, then on the first two samples pooled, then on the first three samples pooled, and so forth. Plot the estimate as a function of number of pooled samples. A well-behaved estimator will level-off, even as sample size is increasing. Just as a raw species accumulation curve can be smoothed by repeatedly randomizing sample order and averaging the curves, the estimate curve can be the average of many randomized sample orders.
The dataset we have been working with was obtained by Project ALAS. The sample for each site is actually a composit of multiple Berlese samples. At each site a sample was taken twice each month for a year (9 sites) or nine months (4 sites). Twentyfive individual Berlese samples were misplaced and the ants from them have never been processed. In lab we will process these samples by identifying the ants and incorporating the new data in the ALAS dataset. We will see if these new data substantially change the conclusions.
I have been working on an inventory of the ant fauna of La Selva, and have produced Web-based identification guides to many of the genera. Copies of the Web-based guide will be available for browsing on the lab computers, and we can use it to identify our ants.
Besuchet, C., D. H. Burckhardt, and I. Loebl. 1987. The "Winkler/Moczarski" eclector as an efficient extractor for fungus and litter Coleoptera. Coleopterists Bulletin 41:392-394.
Colwell, R. K., and J. A. Coddington. 1994. Estimating terrestrial biodiversity through extrapolation. Philosophical Transactions of the Royal Society of London, Series B 345:101-118.
Gotelli, N., and R. K. Colwell. 2001. Quantifying biodiversity: Procedures and pitfalls in the measurement and comparison of species richness. Ecology Letters 4:379-391.
Longino, J. T. 2000. What to do with the data. Pages 186-203 in D. Agosti, J. D. Majer, L. E. Alonso, and T. R. Schultz, editors. Measuring and monitoring biological diversity: standard methods for ground-living ants. Smithsonian Institution Press, Washington, D.C., USA.
Longino, J. T., and R. K. Colwell. 1997. Biodiversity assessment using structured inventory: capturing the ant fauna of a lowland tropical rainforest. Ecological Applications 7:1263-1277.
Longino, J. T., R. K. Colwell, and J. A. Coddington. 2002. The ant fauna of a tropical rainforest: estimating species richness three different ways. Ecology 83:689-702.
Ludwig, J. A., and J. F. Reynolds. 1988. Statistical ecology: a primer on methods and computing. John Wiley and Sons, New York, NY, USA.
Magurran, A. E. 1988. Ecological diversity and its measurement. Princeton University Press, Princeton, New Jersey, USA.
May, R. M. 1975. Patterns of species abundance and diversity. Pp. 81-120 in M. L. Cody and J. M. Diamond (Ed.). Ecology and Evolution of Communities. Belknap Press of Harvard University, Cambridge, Massachusetts, USA.
Pielou, E. C. 1975. Ecological diversity. John Wiley and Sons, New York, NY, USA.
Rosenzweig, M. 1995. Species diversity in space and time. Cambridge University Press, Cambridge, UK.
Taylor, L. R. 1978. Bates, Williams, Hutchinson - a variety of diversities. Pp. 1-18 in L. A. Mound and N. Waloff, eds. Diversity of insect faunas: 9th symposium of the Royal Entomological Society. Blackwell, Oxford, U.K.
The most thorough collection of biodiversity related stats:
Alpha diversity:
Abundance Plot: K-Dominance, Rank
Abundance Model: Log-Series, Broken Stick
Rarefaction
Diversity Indices: Shannon, Alpha, Caswell, Berger-Parker, Simpson, Hill, Margalef, McIntosh
Beta diversity:
SHE Analysis, Species Richness, Chao 1 & 2, Jackknife, Species Distribution
Multivariate: Principal Components, Correspondence Analysis, Cluster Analysis, Non-Metric MDS (not yet implemented)
Comparison: Descriptive Statistics, Kulczynski, Mann-Whitney, Rank Correlation, Correlation, Variance-Covariance, ANOSIM
So far it is freeware, but it is not clear to me if this is only the case because it is still beta-software.
ACE Abundance-based Coverage Estimator of species richness
ICE Incidence-based Coverage Estimator of species richness
ICE_CI_50 + or - term for 95% Confidence Interval for ICE, based
on ICE-SD and 50 randomizations
Chao1 Chao 1 richness estimator
Chao2 Chao 2 richness estimator
Jack1 First-order Jackknife richness estimator
Jack2 Second-order Jackknife richness estimator
Bootstrap Bootstrap richness estimator
MMRuns Michaelis-Menten richness estimator:
estimators
averaged over randomizations (runs)
MMMean Michaelis-Menten richness estimator:
estimators
computed once for mean species accumulation curve
Cole Coleman richness expectation
Alpha Fisher s alpha diversity index
Shannon Shannon diversity index
Simpson Simpson (inverse) diversity index
plus, among other more basic stats, some Shared Species estimators and "Morisita-Horn sample similarity index"
"EcoSim is an interactive computer program for null model analysis in community ecology. EcoSim allows you to test for community patterns with non-experimental data. EcoSim performs Monte Carlo randomizations to create "pseudo-communities" (Pianka 1986), then statistically compares the patterns in these randomized communities with those in the real data matrix."
Has modules for
1.Co-occurrence
2.Niche Overlap
3.Size Overlap
4.Species Diversity
John T. Longino, The Evergreen State College, Olympia WA 98505 USA. longinoj@evergreen.edu
Last modified: 30 December 2003.