Chapter 1 – Looking Behind the Numbers

Chapter 1 Question… Mean, Median, Mode

Masao has graded the final exams from last term. There were 12 people in the class and their scores were, 100, 96, 98, 67, 100, 100, 88, 82, 94, 87, 92, and 99. Please create a stem and leaf plot to show the data, then calculate the mean, median, mode, and range. Which of these numbers best represents the data? Why?

Answers:

67, 82, 87, 88, 92, 94, 96, 98, 99, 100, 100, 100

Test Scores

Mean: 92

Median: 95

Mode: 100

Range: 33

I think the mean does a pretty good job of representing this data. Since a few people got 100, and one person got 67 you might want to include the range too.

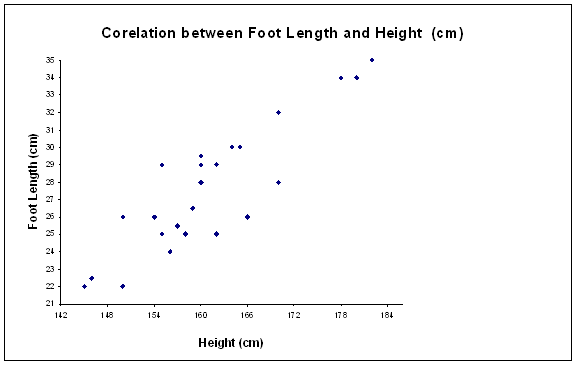
The Mysterious Footprint

   Heather and Seth were excited for the afternoon math class to begin. It was their turn to teach. They had made an especially delicious batch of brownies that morning to be used for one of their assignments. They carefully placed the brownies, along with a bag of flour, down on one of the tables and left the room to fetch paper, markers and other accessories needed for the lesson to run smoothly. Returning with arms loaded with materials, they discovered to their utmost amazement that the brownies had disappeared. The bag of flour had tumbled over spilling all over the floor and interesting enough a footprint, 31 cm long, blatantly starred up at them. Coincidently one of their assignments was to analyze the correlation between foot length and height. So both Seth and Heather quickly got out their graph.

Problem:

1. Analyze the scatter plot above. What type of relationship does it show between heights and foot length? Why did Seth and Heather want to look at this graph? What information did they hope to gain from it?

1. What would you estimate the thief’s height to be?

1. What would you estimate the thief’s height to be for each of the following foot lengths?
1. 27 cm     b. 32 cm     c. 23 cm    

Chapter 2 – Mathematics of Motion

SPEED = DISTANCE divided by TIME

DISTANCE = SPEED x TIME

TIME = DISTANCE divided by SPEED

Laura and Nicole drove for 30 minutes at 40 miles per hour, for 1 hour at 60 miles per hour, and for 20 minutes at 54 miles per hour.

• How far did they travel at each speed?
• What was their total distance?
• Their total time?
• Their total speed?

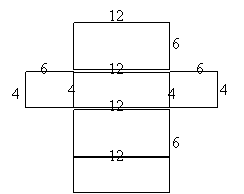
Chapter 3 – Shapes in Space

  6ft 4ft
           12ft

• Draw a net for this rectangular prism.

Note: I recommend that you add the measurements (6ft, 4ft, and 12ft) to your net. It may help you with question number 2.

• Find the surface area of this rectangular prism.

• Find the volume of this rectangular prism

Don’t forget to include the ft, ft 2, and ft 3 in your answers.

Formulas:

Surface area of a rectangle = Length x Width             

w

       l

Volume of a rectangular prism = Length x Width xHeight

h w

       l

ANSWERS TO TEST QUESTIONS

1) There can be various answers to this question.

4

12

2) Surface Area = 24ft 2 + 24ft 2 + 72ft 2 + 72ft 2 + 48ft 2 +48ft 2  

Surface Area = 288ft 2

3) Volume = 12ft x 4ft x 6ft

Volume = 288ft 3

Chapter 4: What Comes Next?

Jana and Kari

1.   Create an addition growth sequence using 1.6 as the starting number and the growth number. Complete 5 steps.

*Answer: 1.6 3.2 4.8 6.4 8

2.   Solve for the growth number and fill in the missing numbers on this addition growth sequence:  

     2 __ __ 11

*Answer:    2 5 8 11

g = (B-A)/N = (11-2)/3 = 9/3 = 3

     g = 3

3.   Find the growth number and the 100 th term for the sequence:

     6 13 20 27 34

*Answer:   Starting number + growth number(n – 1)

     Remember that n = the term you are looking for

     6 + 7 (n – 1) = 6 + 7 (99) = 6 + 693 = 699

     100 th term = 699

3. Describe a way to find the missing numbers in this sequence

5, ___, ____, 17

4.

Fill in the missing numbers:

2, ___, ___, 31.25

What growth number did you use? Was it addition or multiplication sequence?

Seth Vanzant

Chapter 5 - Exploring the Unknown

Test Questions (Evaluating Expressions)

Evaluate each expression for the given values of the variables

1. Evaluate 7x + 2 for:

a) x = 2 b) x = 5 c) x = 3

2.Evaluate x 2 + 4x for:

a) x = 1 b) x = 2 c) x = 6

3.Evaluate 4y – 6 for

a) y = 0 b) y = 4 c) y= ½

4.Write an expression for the collection of Lab Gear blocks below. Then evaluate the expression for the given values of the variables.

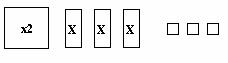
a) x = 3 b) x = 5 c) x = 4

Heather Schuiling

MET

Test Questions for Final Exam

Chapter 6 - Roads and Ramps: Slopes, Angles, and Ratios

• Choose a scale and make an accurate scale drawing using a ruler and a protractor to find the height of the ramp.

Slope angle 30°, length 14m

• Maria measured the angle of elevation to the top of a redwood tree from four different distances: 10ft, 25ft, 48ft, and 60ft. She obtained angles of elevation of 84°, 59°, 64°, and 76°, but the angles are not listed in the correct order. Match each distance with the correct angle of elevation.

Chapter 7 – Family Portrats

If a rock is thrown straight up (say we have a faulty catapult. Whoops!) at a speed of 114 feet per second, its height (in feet) after t seconds will be h = 114t – 19t².

Find the height of the rock after 0, 1, 2, 3, 4, 5, and 6 seconds. Show results in a table.

Use table to plot points and make a graph. Show time on the x axis and height on the y axis.

According to your graph, when does the rock reach maximum height?

When the rock is about 100 feet away from you, you probably ought to step out of the way. How many seconds will it take for the rock to be that close to you?

Which direction does your parabola open? Why?

ANSWERS

• (Need to first work out in class with a protractor)
• 10ft = 84°, 25ft = 76°, 48ft =64°, and 60ft = 59°

Chapter 7 – Family Portraits

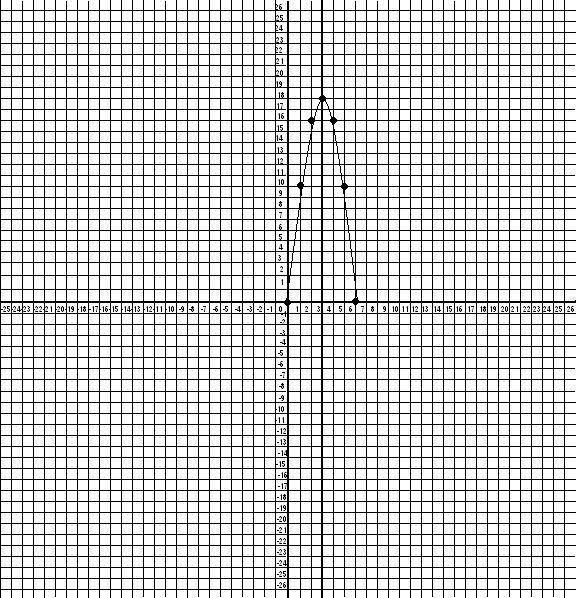
1. Graph this chart:

What is the line of symmetry for this parabola? Show it on your graph.

What is the highest value for x?

Answer to problem #1: (Highest value of x=3.)

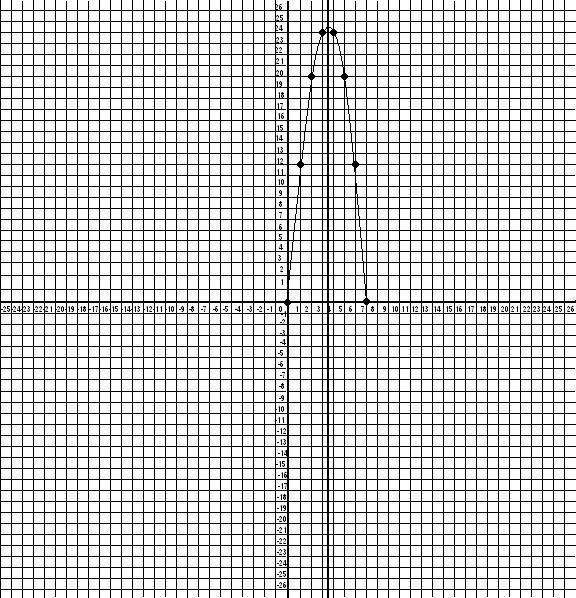
2. Graph this chart:

What is the line of symmetry for this parabola? Show it on your graph.

What is the highest value for x?
Answer to problem #2: (Highest value of x=3.5)

3. Make a t-chart and graph of each of the following equations:

a.       b.

1. y = x²     1. y = -x²  
2. y = 2x²     2. y = -2x²
3. y = ½x²   3. y = -½x²

ANSWER:

ANSWER to #3, continued.

4.

If a rock is thrown straight up (say we have a faulty catapult. Whoops!) at a speed of 114 feet per second, its height (in feet) after t seconds will be h = 114t – 19t².

Find the height of the rock after 0, 1, 2, 3, 4, 5, and 6 seconds. Show results in a table.

ANSWER:

Use table to plot points and make a graph. Show time on the x axis and height on the y axis. (SEE GRAPH BELOW)

According to your graph, when does the rock reach maximum height?

ANSWER: the rock reaches maximum height at 3 seconds.

When the rock is about 100 feet away from you, you probably ought to step out of the way. How many seconds will it take for the rock to be that close to you?

ANSWER: I’ve got 5 seconds to get out of the way!

Which direction does your parabola open? Why?

ANSWER: This is a downward-facing parabola. It is shaped that way because it shows the relationship of gravity upon propulsion and time. You would be able to tell this by looking at the problem, as the coefficient (that’s the second number on the right hand side of the problem,) is negative.

ANSWER to problem #4 continued.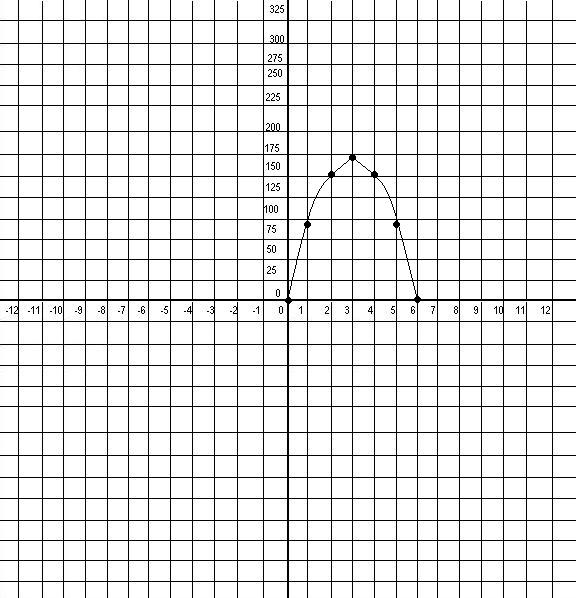

Chapter 8 – Probability

1. A fair 4 sided and 5 sided die are tossed together.
1. List all the possible outcomes
2. What is the probability that the sum of faces is 3?
3. What is the probability that the sum is 5?
4. What is the probability that the sum is 8?
2. A bag contains 2 green beads and 3 orange beads. Two beads are drawn at random.
1. Draw a tree diagram showing the possible outcomes.
2. What is the probability of getting both orange beads?
3. What is the probability of getting one of each color?

Answers:

• (a)1,1; 1,2; 1,3; 1,4, 1,5

2,1; 2,2; 2,3; 2,4; 2,5

3,1; 3,2; ;3,3;3,4; 3,5

4,1; 4,2; 4,3; 4,4; 4,5

1.b 2/20

1.c 4/20

1.d 3/20

\2.