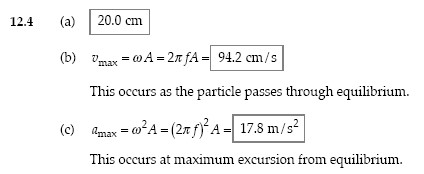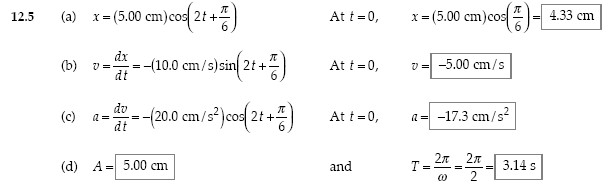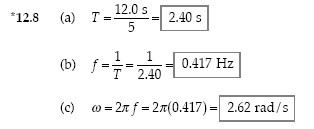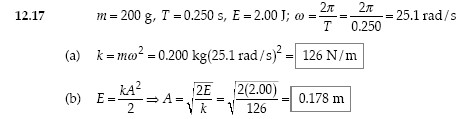Questions
Q12.2 When the spring with two masses is set into oscillation in space, the coil in the exact center of the
spring does not move. Thus, we can imagine clamping the center coil in place without affecting the
motion. If we do this, we have two separate oscillating systems, one on each side of the clamp. The
half-spring on each side of the clamp has twice the spring constant of the full spring, as shown by the
following argument. The force exerted by a spring is proportional to the separation of the coils as the
spring is extended. Imagine that we extend a spring by a given distance and measure the distance
between coils. We then cut the spring in half. If one of the half-springs is now extended by the same
distance, the coils will be twice as far apart as they were for the complete spring. Thus, it takes twice as
much force to stretch the half-string, from which we conclude the half-spring has a spring constant that
is twice that of the complete spring. Our clamped system of masses on two half-springs, therefore, will
vibrate with a frequency that is higher than f by a factor of sqrt(2)
Q12.6
(a) In simple harmonic motion, one-half of the time, the velocity is in the same direction as the
displacement away from equilibrium.
(b) Velocity and acceleration are in the same direction half the time.
(c) Acceleration is always opposite to displacement, never in the same direction.
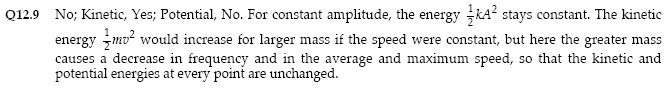
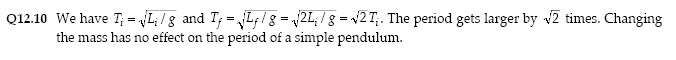
Q12.12 No. If the resistive force is greater than the restoring force of the spring, the
system will be overdamped and will not oscillate.
Problems