Linear algebra

From true

Jump to: navigation, search

Note: This page contains advanced material which is not required for the True, but not Obvious program.

A more advanced mathematical approach to special relativity treats relativistic effects as a vector transformation and uses the approaches of linear algebra to compare the spacetime coordinates in different reference frames.

This method is quite useful and even fun. You might want to give it a try.

Contents

[edit] The math

[edit] Vectors

Vectors are mathematical objects which have both some quantity and some direction. They are often expressed in coordinate systems. So, for spacetime, we have been using coordinates ( t, x ) or more fully ( t, x, y, z ).

[edit] Multiplication

Mathematicians have found a couple useful ways to multiply vectors. One interesting tool in linear algebra is to multiply a vector by a matrix. To do this, you do a two-step process of multiplication and addition for each component of the vector. It may seem confusing at first, but after you do it a few times, it becomes easier. So the only way to learn it is by example.

So, suspend your suspicions for a moment and just take for granted that we can make up a game that goes like this.

Given a thing called a two-dimensional vector 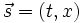\vec{s} = ( t, x ), and a thing we will call a two-by-two matrix 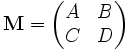\mathbf{M} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} , one can multiply 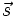\vec{s} times M in the following way

  1. Multiply the first component of the vector times the first element of the first column of the matrix.
  2. Multiply the second component of the vector times the second element of the first column of the matrix.
  3. Add the results of Steps 1 and 2; the result is the first component of the result vector.
  4. Multiply the first component of the vector times the first element of the second column of the matrix.
  5. Multiply the second component of the vector times the second element of the second column of the matrix.
  6. Add the results of Steps 4 and 5; the result is the second component of the result vector.


Mathematically, it looks like this.

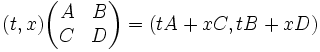
( t, x ) \begin{pmatrix} A & B \\ C & D \end{pmatrix} = (t A + x C, t B + x D)

A meaningless numerical example:

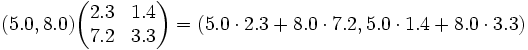
( 5.0, 8.0 ) \begin{pmatrix} 2.3 & 1.4 \\ 7.2 & 3.3 \end{pmatrix} = ( 5.0 \cdot 2.3 + 8.0 \cdot 7.2, 5.0 \cdot 1.4 + 8.0 \cdot 3.3 )

= ( 11.5 + 57.6, 7.0 + 26.4 )

= ( 69.1, 33.4 )

The interesting thing here is that you can take a vector, multiply it by something, and end up with another vector.

[edit] An Application: Spacetime

Now to bring linear algebra together with the time stretch factor.

If you create the transformation matrix

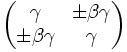
\begin{pmatrix} \gamma & \pm \beta \gamma \\ \pm \beta \gamma & \gamma \end{pmatrix}

Then you can transform the spacetime vector ( t, x) viewed in one frame into the spacetime vector viewed from another frame moving with a velocity β relative to the first.

Whether you use the matrix which has the positive or negative elements depends on the direction of the relative velocities of the frames, but there are either four positive elements or two positive and two negative elements.

[edit] A time dilation example

  • Two frames are traveling with a relative velocity of 0.6c.
  • Event 1 is taken as the origin in both frames.
  • Event 2 is observed to have the coordinates (5 m, 3 m) in one frame.
  • What are the coordinates of Event 2 in the other frame?

We want to multiply the spacetime vector times the transformation matrix.

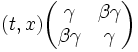
( t, x ) \begin{pmatrix} \gamma & \beta \gamma \\ \beta \gamma & \gamma \end{pmatrix}

We have

t = 5 m
x = 3 m
β = 0.6
\gamma = \frac{1}{\sqrt{1-\beta^2}} = 1.25
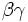\displaystyle \beta \gamma = 0.75

So we multiply

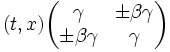
( t, x ) \begin{pmatrix} \gamma & \pm \beta \gamma \\ \pm \beta \gamma & \gamma \end{pmatrix}


= ( 5 m, 3 m ) 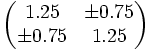\begin{pmatrix} 1.25 & \pm 0.75 \\ \pm 0.75 & 1.25 \end{pmatrix}

= ( 6.25 m \pm 2.25 m, \pm 3.75 m + 3.75 m )

= ( 8.5 m, 7.5 m ) or ( 4.0 m, 0.0 m )

Which of these two answers is correct? That depends on the situation. Both are possible ways of viewing Event 2 from a frame that is moving at 0.6c relative to the first frame. In one case, the second frame is moving in the -x direction relative to the first frame which creates coordinates for Event 2 which are even further in the +x direction: ( 8.5 m, 7.5 m ). In the other case, the second frame is moving in the +x direction relative to the first frame which allows Event 2 to happen at the spatial origin of the second frame but at a slightly later time: ( 4.0 m, 0.0 m ).

Notice that the interval between Event 1 and Event 2 is the same for all three frames. Numerically, the interval is 4.0 m.

Can you see how the transformation matrix is actually just another version of the interval? Work it out!

Retrieved from "http://www2.evergreen.edu/wikis/true/index.php?title=Linear_algebra"