Pythagorean Theorem

From true

Jump to: navigation, search

The Pythagorean Theorem is the basis for a lot of the activities we will do in this class. Getting used to using it is an easy way to build up your confidence with algebra while exercising the visual-spatial parts of your mind.

[edit] The Equation

The mathematical shorthand which summarizes the Pythagorean Theorem is

a2 + b2 = c2.

But to understand this, your mind must expand the shorthand into its full meaning. What the equation means only makes sense in the context of right triangles where a and b are the lengths of the two legs of the right triangle and c is the length of the hypotenuse (or longest side) of the right triangle.

So, to repeat...

  • the equation only works for right triangles;
  • you must associate the letters in the equation with lengths; and
  • you must associate c with the length of the longest side.

[edit] Applications

One of the most useful applications of the Pythagorean Theorem is in the calculation of distance when the position of an object is known relative to a rectangular coordinate system.

[edit] Examples

Q. If you are sure that you have a right triangle with legs that are 14 cm and 8 cm long, how long is the hypotenuse?

A.

a2 + b2 = c2 
142 + 82 = c2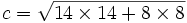
c = \sqrt{14 \times 14 + 8 \times 8}
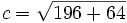
c = \sqrt{196 + 64}
c = \sqrt{260}
c = 16.1

Since the units were centimeters in both the measurements of the legs, the answer is 16.1 cm.

Q. If you know the longest side of a right triangle measures 0.5 m and one of the legs is 0.25 m long, how long is the other leg?

A.

a2 + b2 = c2 
a2 + 0.252 = 0.52
a2 = 0.52 − 0.252
a = \sqrt{0.5 \times 0.5 - 0.25 \times 0.25}
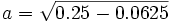
a = \sqrt{0.25 - 0.0625}
a = \sqrt{0.1875}
a = 0.433

Since the units were meters in both the measurements of the legs, the answer is 0.433 m or 43.3 cm.

Retrieved from "http://www2.evergreen.edu/wikis/true/index.php?title=Pythagorean_Theorem"