Do parts A and B below;  leave C for the very end in case you have extra time, maybe design some investigations of your own... and turn in the survey before you leave. Have fun!

• To experience image formation by lenses.
• To better understand the behavior of light.
• To build a telescope.
• To understand how a simple refracting telescope works
  

(B) Make a telescope:  If you remove the screen, the real image is still there in space, and it can be examined with a magnifying glass. That is a telescope.

(C) Further investigations:  Play with different lenses.  If you have time, investigate how the relative positions (and focal lengths) of lenses affect image locations and sizes, more carefully and quantitatively.

• assorted lenses and/or magnifying glasses
• blank 3x5 cards
• rulers and meter sticks
• a lamp to shine on a clock on the wall
• illuminated arrows, lens holders, optical benches (if available)

---

DETAILS:

(A) A real image forms at the focal point of a convex lens.

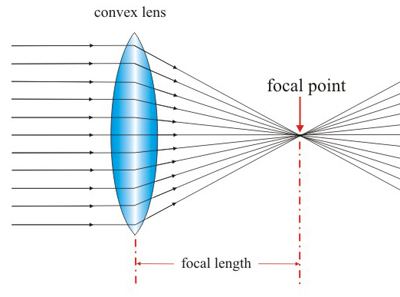
Light bounces off a tree (for example) in all directions. The few light rays that reach you from a distant tree are traveling nearly parallel to each other. When those parallel rays come through your lens, the lens will focus them at some point in space. If you move a blank card to that point, you can see that the focused rays form an image (on the card) of your object (the tree).  The focal length is the point at which the lens will focus distant light (parallel rays) into an image.  The focal length (f, or focal point) of a lens turns out to be half the radius of curvature R of the lens (Fig.a).

9

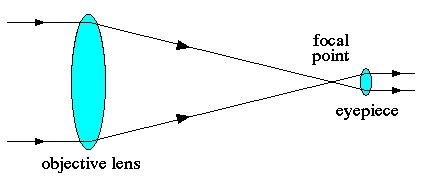Fig.(a) Convex lens	Fig.(b) Refracting telescope made of two convex lenses

Measure the focal lengths of several lenses: Choose convex lenses to start with. You can feel that they curve out, not in (concave), on both sides, even if you can't see the curvature.

• Go to the window or stand outside in the shade. Choose a distant, sunlit object such as a tree.
• Hold a lens in one hand and a blank 3x5 card in the other. Vary the distance between them until a clear image forms on the card.  Is the image upright or inverted?  What else do you notice about the image?  Light rays actually converge in space at the position of this image, so we call it a 'real' image. The screen reflects these light rays into your eyes (and other directions).
• Have a partner measure the distance between the card and the (center of) the lens. Write down the focal length of each lens.
• Discuss what you see and record your observations.
Imagine putting camera film or your retina in place of the card. The light of the image excites an electromagnetic or chemical response on the surface it impacts. Notice that the point where objects focus appears independent of their color or size. *********************************************************************

(B) A simple refracting telescope has an eyepiece near the focal point of the objective lens (Fig.b)

• Get two convex lenses, one highly curved (small f2: the eyepiece) and a flatter one, with a very slight curve (large f1: the objective lens).   You might use a magnifying glass for one of your convex lenses.
• Fix the flatter objective lens on the optical bench and use your 3x5 card to find the image of a distant object (e.g. an illuminated wall clock inside, if the trees outside are too dim).  If you don't have an optical bench, have one partner hold the lens still at the 0 end of a meter stick, and the other partner measure the location of its image (f1).
• Check the focal length of your smaller lens (f2).
• Then place your highly curved eyepiece lens so that its focal point is at the objective's focal point. See Fig.b. What is the total distance between the (center of) the two lenses, in terms of f1 and f2?
• Look straight through the eyepiece and the objective, at your distant object.  The eyepiece will direct the image light into your eyes as parallel rays. Does it look like the object is closer or further? Larger or smaller? Move the lens and your eye around until you can see the effect clearly.  Help your partner see it.
• Discuss what you see and write down your observations.

Magnification: Try to see the clock itself in the same field of view as your magnified image of the clock, one with each eye. Estimate how much bigger the image appears than the object. The ratio M= (-image size/ object size) is the magnification. (The minus sign is for the orientation of the image: is it right side up or upside down?)

How does M compare to the ratio of your lenses' focal lengths?

Extra:  look through your neighbors' telescopes.  How does their magnification compare with yours?  What does this have to do with the ratio of the focal lengths of their lenses?

*********************************************************************

C: More advanced investigations - optional

(C.0) It's also possible to make a telescope with a concave eyepiece. Try it if you have time. What size works for your objective? Do you notice any difference in the image?

(C.1) You have seen that images of distant objects form at the focal point of a lens.  Images of close objects form not at the focal point, but at a point that depends on the distance between the object and the lens. The lighted arrows are convenient objects for investigating this. Mount a lighted arrow on one end of the optical bench, and a card on the other (no lens yet). Move the card back and forth; can you get an image of the arrow to focus clearly on the card? Now choose a lens to mount between the card and the lighted arrow, at some arbitrary distance.
(a) Move the lens and/or the card around until you get a clear image of the arrow on the card. Measure the object distance, p, between the object and the lens, and the image distance, q, between the image and the lens, and keep track of them.
(b) Move the lens away from the light (increase p). Where do you have to move the card to find the image? Does q increase or decrease? Does the image get bigger or smaller?
(c) Remember to record the focal length f of your lens.
(d)  Discuss your observations and write down a sentence that summarizes  - in words - how the object distance depends on the image distance.

(C.2) Thin lens equation: (1/f) = (1/p) + (1/q)

Check this relation by calculating (1/p) + (1/q) for (a) and (b) above. How do your results compare to the focal length f of your lens?  The results may not match perfectly.  Why not?

(C.3) Magnification M=(-q/p) = relative size of image, compared to object, as you may have discovered above. Since the image and the object subtend the same angle from the lens, the larger is further away. An object close (small p) to the lens (but not inside the focal length...) yields a large image (large q) far from the lens (consider a magnifying glass). An object far from the lens (large p) yields a small image close to the lens (small q). Calculate the magnification M for your setup above. How does it compare to your observations about the relative size of the image and object, and their respective distances from the lens?

(C.4) Signs: Your p and q (and f) are positive numbers (for real objects and images, and converging lenses), so your M is negative. Does negative M correspond to an upright or inverted image?

(C.5) Predictions and tests: Pick a different lens whose f you know. Mount it a fixed distance p (greater than f) from your lighted arrow. Use the simple equation above to predict where the image will be (calculate q). Check your prediction by moving the card around until you find the image, to measure q. How do your results compare? How does the magnification change?  What could contribute to a slight mismatch between your calculations and your observations?

---

Please fill out the survey about the workshop:  What surprised you?  What did you learn?  What new questions or ideas do you have?


---

Return to Astronomy homepage         


---

Maintained by:  E.J. Zita