Dr. Akihiro Sumida

Explanation of the data sets of skeleton trees

The objective of the study is to investigate the effects of spatial structure (skeleton structure of trunks and branches) on neighborhood competition patterns among hardwood trees. Results will soon be published from Annals of Botany. In the following the method of measurements is mainly summarized for my data sets to be understood.

Study plot and equipments
In a hardwood forest, three-dimensional coordinates (x, y, z) were settled in the study plot with an area of about 20 m x 25 m, with positive direction of y being north and z vertical. The plot included 10 canopy trees of Japanese chestnut Castanea crenata. Crowns of 16 other canopy trees (7 species) neighbored those of C. crenata.
To survey tree structure, we used a theodolite equipped with a visible (red) laser range finder. With the range finder, measurement for distances up to 60 m is possible without a reflector. With the visible laser we can confirm where we are aiming (or to which distance we are measuring) even in a dense forest. Three-dimensional coordinates of the target where red laser is spotted is automatically calculated, displayed on the monitor of the theodolite, and stored in a pocket computer.

Surveying a tree
For most of the primary branches (= stems branching off the main trunk) of the chestnut trees, three-dimensional positions of their base, tip, and several turning points of branch direction were measured using the theodolite. Primary branches around the top of a trunk (about 2 m from treetop) were not always measured because they were relatively short and so often invisible. For species other than C. crenata, only the primary branches extending towards neighboring C. crenata trees were surveyed. Position measurement for the trunk was made for trunk base, 1.3-m height point, and the treetop other than the junctions of the primary branches. Since the laser was aimed on the surface of branches and trunks, measured positional data do not represent internal positions of tree body. Hence we rounded the position data to nearest 10 cm. However, because of the large size of trees, this procedure does not affect essential results. The theodolite was set at multiple points (“survey points”) on the forest floor to survey from different sides of a single tree.

Unification of 3-D coordinates
Since the built-in frame of reference of the theodolite changes every time it is moved to a different “survey point”, the coordinates of all these survey points needed to be linked with one another. Therefore, arbitrarily chosen fifteen points (“reference points”) were further set on the forest floor, and the three-dimensional coordinates of these reference points were determined by ordinary closed traverse survey. Then the positions of the survey points were surveyed from some of the reference points to link them together. In this way, all the three-dimensional data were finally converted into the unified coordinates of the study area. It took us a total of 20 days (between July and early December) to carry out all the field measurements.

Visualization
With the three-dimensional data obtained, the skeleton structure of the tree was visualized on a personal computer using a three-dimensional line-graphics facility of graphics package (DeltaGraph, Japan Poladigital). 3-D coordinates of the measured points were input and arranged on a Excel spreadsheet before they were copy-and-pasted onto a DeltaGraph spreadsheet. On a 3-D graphics plane of DeltaGraph, two data points were linked by a line in order of data row; For example, imagine point 1 (x1, y1, z1) shows branch base, point 2 (x2, y2, z2) a turning point of branch direction and point 3 (x3, y3, z3) the branch tip. Then we input (x1, y1, z1) in the first row, (x2, y2, z2) in the second row and (x3, y3, z3) the third row. DeltaGraph automatically connects these three points in this order with two line segments. Therefore, the data sets for visualization are simply made of a sequence of rows of 3-D data points of trunks and branches. An example of the visualization is available at the homepage of my lab ( http://www.lowtem.hokudai.ac.jp/plantecol/home-e.html ; note, the picture is not of the chestnut forest but that of an oak forest).

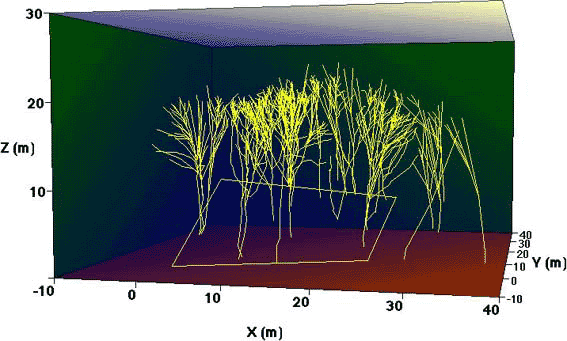
Three-dimensional spatial structure of the trunk and branches of a broad-leaved forest reconstructed from data measured using the Theodorite laser surveyor. The yellow rectangle outlines the survey area (25mX20m)

Analyses
Several analyses were made to evaluate effects of the presence of nearby branches on chestnut crown expansion. One of them includes an analysis for extending direction (branch vector) of each branch. I think data sets that can represent “vector” (connection between 3-D points) are important for explaining present structure and predicting future structure.